• Înțelegerea noțiunii de backtracking
• Implementarea metodei backtracking in rezolvarea problemelor

Noțiunea de backtracking se referă la utilizarea unui algoritm recursiv pentru soluționarea unei probleme ce admite soluții parțiale. Se începe cu una din bucățile de soluție disponibile și se avansează până la construirea soluției complete. Dacă una din rutele de construcție disponibile nu duce nicăieri, se merge înapoi (backtrack) și se încearcă altă cale. Dacă niciuna din rute nu dă o soluție, atunci problema nu este rezolvabilă.

Algoritmul generat este următorul:

Dată fiind o matrice 2D de caractere, să se verifice dacă există un cuvânt în matrice. Dacă da,să i se afișeze calea. Se permite mișcarea în toate cele 8 direcții.

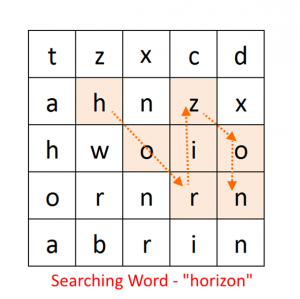
Procedeu:

• Se creează o matrice de soluție
• Se ia fiecare celulă a matricei de caractere ca punct de plecare
• Se verifică dacă celula curentă nu face parte din soluție și dacă litera conținută se potrivește cu litera din cuvânt la care s-a ajuns printr-o variabilă index care începe cu 0.
• Se verifică toate cele 8 direcții și se are în vedere să nu se depașească marginea matricei
• Dacă index = lungimea cuvântului, se afișează soluția
• Dacă nu, dar se verifică pasul 3, se pune un număr în căsuța corespunzătoare din matricea de soluție (numerele se vor pune în ordine crescătoate/descrescătoare ca să se rețină ordinea caracterelor).
• Se aplică recursiv algoritmul pentru index + 1
• Dacă niciuna din cele 8 căsuțe nu corespunde vreunei litere din cuvânt,se dă înapoi și se marchează celula din matricea de soluții ca neutilizată.
• Se schimbă punctul de start.

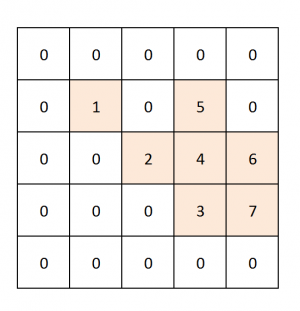
Mai jos este matricea de soluții pentru căutarea cuvântului „horizon“ în cea de mai sus.
Se notează cu 0 celulele neutilizate.

Fiind dar un și de caractere și un dicționar de cuvinte, să se verifice dacă șirul poate fi spart în cuvinte din dicționar și ,dacă da, să se afișeze acestea cu spațiu între ele.

Procedeu naiv:

• Se navighează prin șirul de caractere de intrare
• Se ia un șir gol și se adaugă caracter cu caracter la el
• Se verifică încontinuu dacă șirul există în dicționar
• Dacă da, se adaugă șirul la răspuns și se apelează funcția pentru restul șirului de intrare
• Dacă la un moment dat nu se mai pot găsi cuvinte, se dă înapoi și se elimină ultimul cuvânt din răspuns și se continuă adăugarea de caractere de la el înainte
• Dacă s-a ajuns la sfârșitul șirului de intrare și toate caracterele sunt intr-un cuvânt din răspuns, înseamnă că șirul a fost spart cu succes.

Procedeu cu programare dinamică:

• Înainte de a ne apuca de rezolvarea oricărui string construit verificăm dacă nu l-am rezolvat deja.
• De fiecare dată când un string construit nu poate fi descompus în cuvinte, il ținem minte pentru a nu-l mia verifica data viitoare.
• Mai jos este un exemplu cu ce s-ar întâmpla fără programarea dinamică

1. Generarea produsului cartezian A^N (interpretare: toate numerele de N cifre, dar cu cifrele alese numai din mulțimea A). Exemplu: A = {1,2,3}, N = 6;
2. Generarea tuturor permutărilor de N;
3. Generarea tuturor combinărilor/aranjamentelor de N luate câte k;
4. Problema calului pe tabla de şah;
5. * Problema turelor pe tabla de şah;
6. Problema reginelor pe tabla de şah;
7. Găsirea unui lanţ Hamiltonian într-un graf;
8. * Găsirea unui ciclu Hamiltonian într-un graf;
9. Problema comisului-voiajor;

Pentru acest laborator puteți descărca scheletul de cod de aici. Descărcați arhiva și dezarhivați-o.

Puteti folosi utilitarul wget pentru descarcare si utilitarul unzip pentru dezarhivare.

• wget http://elf.cs.pub.ro/sda-ab/wiki/_media/laboratoare/lab12_backtracking-skel.zip
• unzip lab12_backtracking-skel.zip

Pentru compilare folositi comanda make.