Unelte utilizator
Bara de navigare
Cuprins
Laborator 07: Arbori minimi de acoperire
1. Obiective laborator
- Înțelegerea conceptului de arbore minim de acoperire
- Înțelegerea implementării algoritmilor care determină acest arbore
- Înțelegere aplicațiilor practice în:
- rețele de calculatoare: obținerea unui cost redus la interconectarea mai multor stații (ex: protocolul STP folosit în LAN-uri)
- prelucrarea de imagine: segmentarea cadrelor (ex: folosită în analiza medicală)
- în clustere: determinarea unei topologii de comunicare, în cazul în care topologia nu era una regulată(arbore, inel)
2. Introducere
2.1 Conexitate în grafuri
Componentă conexă
O componentă conexă a unui graf neorientat este un subgraf cu următoarele proprietăţi:
- oricare două noduri din acest subgraf sunt conectate(există un lanţ între ele)
- orice nod din acest subgraf NU este conectat cu niciun nod din afara subgrafului(nodurile din componentă fac muchii numai cu alte noduri din componentă)
Graf neorientat conex
Un graf neorientat este numit conex dacă are o singură componentă conexă.
Graf orientat slab conex
Fie graful neorientat asociat unui graf orientat obţinut prin înlocuirea tuturor arcelor cu muchii. Atunci un graf orientat este slab conex dacă graful neorientat asociat acestuia este conex.
Graf orientat tare conex
Un graf orientat este tare conex dacă există drum între oricare două noduri, atât într-un sens, cât şi în celelalt.
Se pot defini similar componentele slab conexă şi tare conexă.
2.2 Arborele văzut ca graf
Folosind noţiunile de mai sus, putem spune că un arbore este un graf(pentru simplitate, fie neorientat) conex şi cu număr minim de muchii, prin urmare, aciclic.
2.3 Arbore vs. pădure de acoperire
Pentru un graf neorientat, construirea unui arbore de acoperire(nu neapărat de cost minim) presupune construirea unui arbore care să fie graf parţial(să acopere toate nodurile).
Acest lucru este posibil numai dacă graful este conex. În caz contrar, se poate construi câte un arbore de acoperire pentru fiecare componentă conexă a grafului, spunând că se construieşte o pădure de acoperire pentru graf.
2.4 Arbore de cost minim
Dacă fiecare muchie dintr-un arbore are un cost(o pondere), atunci costul arborelui este dat de suma costurilor muchiilor ce formează arborele.
Dacă, pe acelaşi principiu, fiecare muchie dintr-un graf are un cost, atunci alegerea unui arbore minim de acoperire presupune alegerea unui arbore care să acopere toate nodurile şi care să folosească muchiile ce dau suma costurilor minimă.
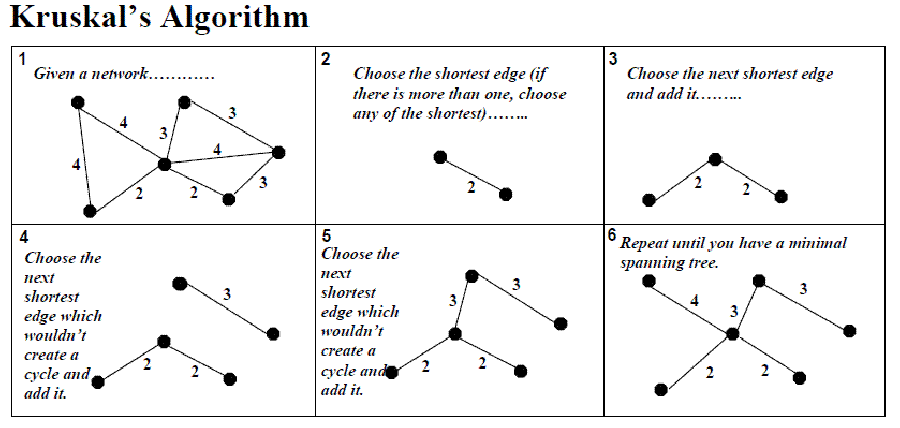
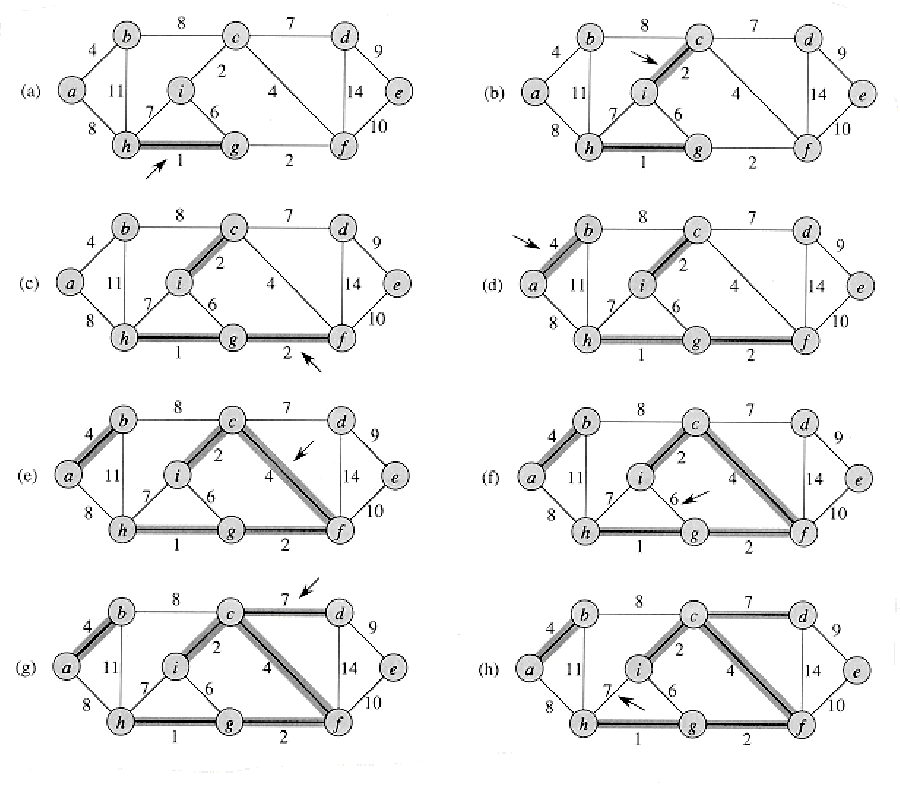
3. Algoritmul lui Kruskal
Algoritmul lui Kruskal este un algoritm în teoria grafurilor care găsește arborele parțial de cost minim pentru un graf conex ponderat.
Cu alte cuvinte, găsește submulțimea muchiilor care formează un arbore care include toate vârfurile și care este minimizat din punct de vedere al costului.
Dacă graful nu este conex, atunci algoritmul găsește o pădure parțială de cost minim (un arbore parțial de cost minim pentru fiecare componentă conexă). Algoritmul lui Kruskal este un exemplu de algoritm greedy.
- creează o pădure F (o mulțime de arbori), unde fiecare vârf din graf este un arbore separat
- creează o mulțime S care conține toate muchiile din graf
- atât timp cât S este nevidă
- elimină o muchie de cost minim din S
- dacă acea muchie conectează doi arbori distincți, atunci adaugă muchia în pădure, combinând cei doi arbori într-unul singur
- altfel, ignoră muchia
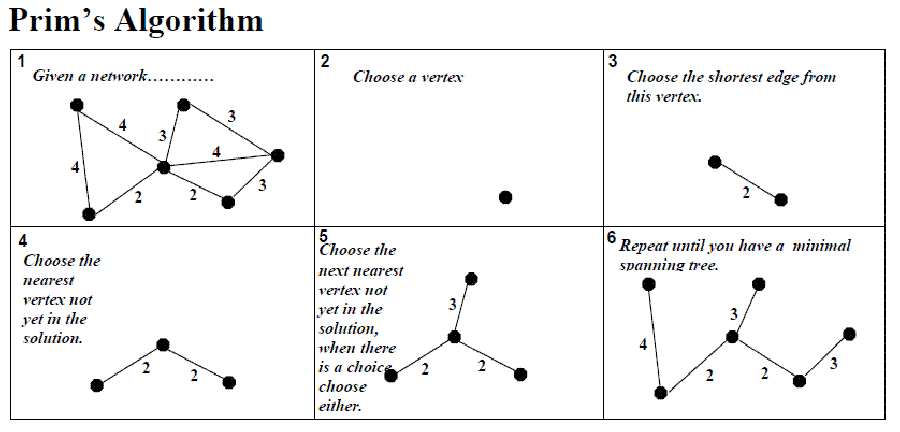
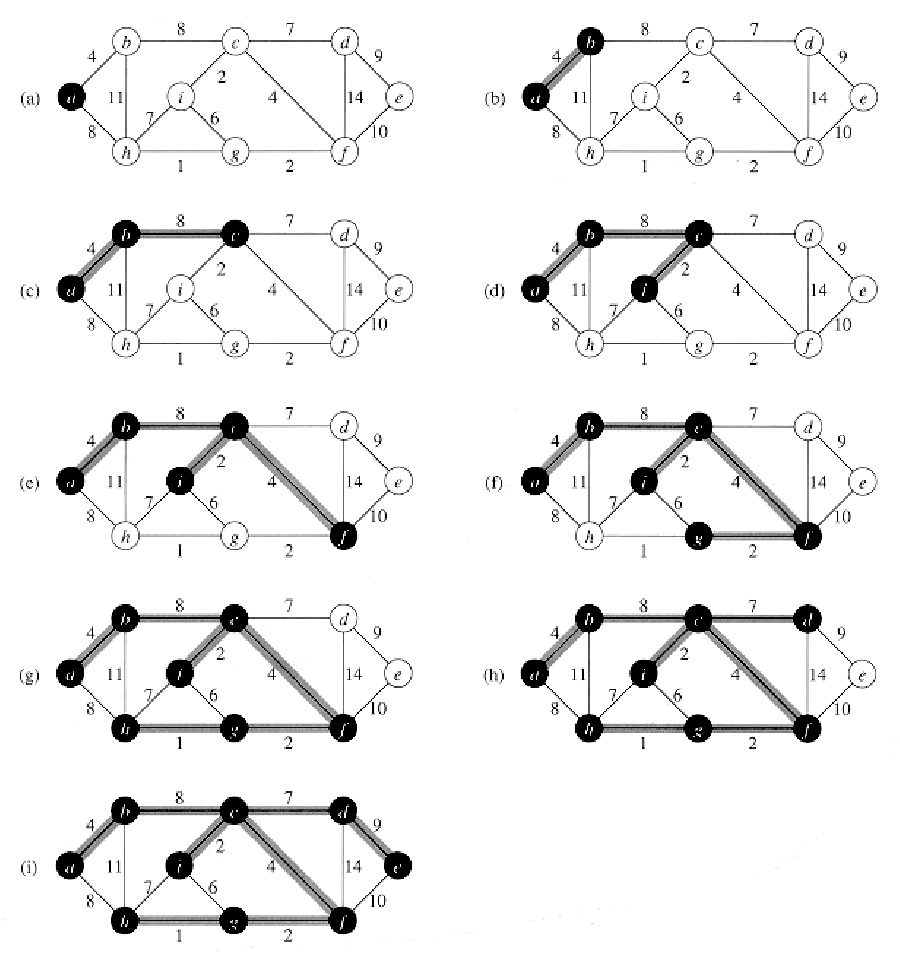
4. Algoritmul lui Prim
Algoritmul lui Prim este un algoritm din teoria grafurilor care găsește arborele parțial de cost minim al unui graf conex ponderat. Înseamnă că găsește submulțimea muchiilor care formează un arbore care include toate vârfurile și al cărui cost este minimizat.
- Intrare: Un graf conex ponderat cu nodurile V și muchiile E.
- Initializare: Vnou = {x}, unde x este un nod arbitrar (punct de plecare) din V, Enou= {} repetă până când Vnou=V:
- Alege muchia (u,v) din E de cost minim astfel încât u este în Vnou și v nu e (dacă există mai multe astfel de muchii, se alege arbitrar)
- Se adaugă v la Vnou, (u,v) la Enou
- Ieșire: Vnou și Enou descriu arborele parțial de cost minim
5. Exerciții de laborator
1.Vi s-a asignat rolul de nou coordonator al departamentul de rețelistică al companiei Coca Cola (Pepsi petru cei cărora nu le place Cola). Sediul companiei are arondate N-1 sucursale, iar voi trebuie să asigurațu conectivitate între toate locațiile folosind o lungime minimă de fibră optică, lucru care duce implicit la reducerea costurilor totale.
# explicatii format # n=numar varfuri m=numar muchii # m randuri, cate unul pentru fiecare muchie: start end cost 8 13 1 2 4 1 3 9 1 4 1 1 6 7 2 3 12 2 4 4 3 8 13 4 5 7 4 6 8 5 6 3 5 7 6 5 8 5 7 8 2
5.1. Exerciții - schelet de laborator
Pentru acest laborator puteți descărca scheletul de cod de aici. Descărcați arhiva și dezarhivați-o.
Linux
Puteti folosi utilitarul wget pentru descarcare si utilitarul unzip pentru dezarhivare.
wget http://elf.cs.pub.ro/sda-ab/wiki/_media/laboratoare/lab6_arbori_min-skel.zipunzip lab6_arbori_min-skel.zip
Pentru compilare folositi comanda make. Pentru rulare puteti folosi comanda make run sau ./graph.
Extra
- Se dă un graf care coincide cu un arbore minim de acoperire. Verificaţi dacă, introducând o nouă muchie în graf, costul arborelui minim de acoperire se schimbă şi, dacă da, găsiţi muchia ce va fi scoasă.
- Se dă un graf care coincide cu un arbore minim de acoperire şi un vector(V) cu K noduri din graf. Care este costul minim al muchiilor pe care trebuie să le eliminaţi din graf pentru ca fiecare nod din vectorul V să se afle în altă componentă conexă. (Să nu existe drum între oricare două noduri din vectorul V).
- Se dă un graf care coincide cu un arbore minim de acoperire şi un nod auxiliar care formează doar două muchii. Verificaţi dacă folosirea nodului auxiliar pentru a conecta nodurile duce la un arbore de acoperire cu un cost mai mic.