• Înțelegerea ideii de cost și de drum minim într-un graf
• Prezentarea algoritmilor care calculează drumul de cost minim
• Înțelegerea aplicațiilor practice prezente în:
  • găsirea drumului minim între 2 locații (ex: GPS)
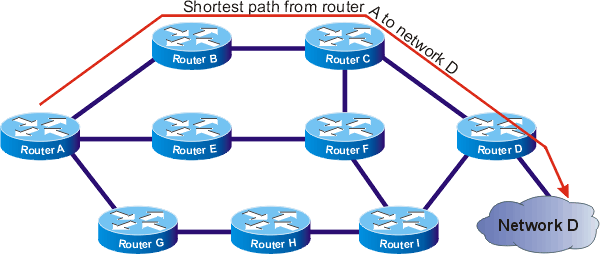
  • rutarea în cazul rețelelor de calculatoare (ex: protocolul RIP)

La fel ca la arbori de acoperire, presupunem că fiecare muchie are un cost de parcurgere.

Într-un graf, orice drum este definit de o succesiune de muchii (cu proprietatea că, pentru oricare două muchii consecutive din succesiune, nodul destinaţie/de sosire al primei muchii este acelaşi cu nodul sursa/de plecare al celei de-a doua muchii).

Costul unui drum va fi definit ca suma costurilor muchiilor ce compun acel drum.

Fie un nod sursă(S) şi un nod destinaţie(D). Pot exista mai multe drumuri de la S la D(drumuri care au S = primul nod, D = ultimul nod), iar drumul de cost minim de la S la D va fi cel mai ieftin(cu costul cel mai mic) dintre acestea.

Următorii algoritmi caută drumurile de cost minim de la un singur nod(sursă) la toate celelalte noduri. Rezultatul acestor algoritmi este un arbore cu drumuri de cost minim, unde:

• nodul sursă(S) este rădăcina arborelui;
• toate nodurile din graf sunt în arbore;
• pentru orice nod destinaţie(D), costul drumului din arbore de la rădăcina S la D este drum de cost minim(de la S la D) în graf.

Algoritmul lui Dijkstra se bazează pe un principiu similar cu cel al algoritmului lui Prim:

• iniţial, toate nodurile sunt neexplorate şi vom construi arborele, începând de la nodul S;
• atribuim un posibil cost(o estimare a distanţei) pentru fiecare nod. (iniţial, S are costul 0, toate celelalte noduri au costul infinit);
• la fiecare pas, alegem cel mai bun candidat dintre nodurile neexplorate, urmând să îl explorăm(să îi evaluăm vecinii), iar acel candidat va rămâne în arbore;
• la fiecare explorare(evaluare a vecinilor), dacă găsim o nouă estimare de cost mai bună decât cea precedentă, folosim, mai departe, noua estimare. Dacă dorim să ţinem evidenţa muchiilor folosite, actualizăm şi nodul părinte al vecinului respectiv.

Diferenţa apare, în algoritmul lui Dijkstra, la funcţia folosită pentru estimarea costurilor, atunci când evaluăm vecinii unui nod:

• Dacă C este nodul curent(pe care îl explorăm), atunci:
• pentru fiecare nod vecin(V) al lui C, noul cost posibil va fi costul drumului S-V(de la S la V) care trece prin C, mai exact - suma dintre costul drumului S-C şi costul muchiei (C,V).

Paşii algoritmului lui Dijkstra:

1. Declarăm două mulţimi:
	mulţimea nodurilor neexplorate(MN), iniţial MN conţine toate nodurile;
	mulţimea nodurilor explorate(ME) ce compun arborele, iniţial ME = vidă;
2. Atribuim fiecărui nod o estimare iniţială a costului:
	0 pentru nodul sursă(S);
	infinit pentru toate celelalte;
3. Cât timp există noduri în MN
	1. Alegem, din MN(nodurile neexplorate), nodul cu cel mai mic cost estimat
	 îl numim C(nodul curent)
	2. pentru fiecare din vecinii lui C care se află în MN 
	3. calculăm noua estimare de cost = cost(drumul S-C) + cost(muchia (C,V));
	4. comparăm noua estimare cu vechiul cost(drumul S-V):
	 dacă noul cost e mai bun
		1. actualizăm cost(drumul S-V) = noul cost;
		2. actualizăm parinte(V) = C; (pentru păstrarea muchiei folosite)
	 altfel păstrăm vechiul cost
	5. Marcăm nodul C ca explorat: îl eliminăm din MN şi îl adăugăm în ME.
	 (Nu va mai fi verificat)

Principii similare pentru algoritmul Bellman-Ford:

• vom construi arborele, începând de la nodul S;
• atribuim un posibil cost(o estimare a distanţei) pentru fiecare nod. (iniţial, S are costul 0, toate celelalte noduri au costul infinit);
• la fiecare evaluare, dacă găsim o nouă estimare de cost mai bună decât cea precedentă, folosim, mai departe, noua estimare. Dacă dorim să ţinem evidenţa muchiilor folosite, actualizăm şi nodul părinte.
• funcţia de estimare a costului este definită la fel ca la algoritmul lui Dijkstra(costul drumului de la S la nodul respectiv)

Diferenţa apare, în algoritmul Bellman-Ford, la alegerea nodurilor pentru care facem evaluarea:

• Algoritmul nu are preferinţe pentru anumite noduri şi nu extrage, la fiecare pas, cel mai bun candidat.
• În schimb, acest algoritm evaluează toate muchiile la un pas. Folosindu-se de principiul de mai sus, (N-1) astfel de paşi vor fi suficienţi.

Paşii algoritmului Bellman-Ford:

1. Atribuim fiecărui nod o estimare iniţială a costului:
	0 pentru nodul sursă(S);
	infinit pentru toate celelalte;
2. Executăm de N-1 ori:
	1. Pentru fiecare pereche (u, v) a.i. există muchie de la u la v
		1. calculăm noua estimare de cost = cost(drumul S-u) + cost(muchia (u,v));
		2. comparăm noua estimare cu vechiul cost(drumul S-v):
		 dacă noul cost e mai bun
			1. actualizăm cost(drumul S-v) = noul cost;
			2. actualizăm parinte(v) = u; (pentru păstrarea muchiei folosite)
		 altfel păstrăm vechiul cost

Următorul algoritm caută cel mai scurt drum de la orice nod sursă(S) la fiecare nod destinaţie(D).

Rezultatul algoritmului este o matrice N x N(unde N = |V|, numărul de noduri), iar valorea din matrice de la poziţia [i][j] va fi costul minim pentru drumul i-j. Fie această matrice numită dist.

Pentru simplitate, algoritmul numerotează nodurile de la 1 la N şi foloseşte următoarea construcţie:

• defineşte o funcţie costMinim(i,j,k) = cel mai ieftin drum care:
• -pleacă din i
• -ajunge în j
• -în afară de primul şi de ultimul nod, conţine numai noduri din {1,2,3,…,k}(primele k noduri).

Algoritmul calculează costMinim(i,j,k) pentru toate perechile (i,j,k), folosind formula: costMin(i,j,k+1) = min(costMin(i,j,k), costMin(i,k+1,k) + costMin(k+1,j,k));

Paşii algoritmului Floyd-Warshall:

1. Declarăm matricile:
	dist, matrice N x N şi o iniţializăm dist[i][j] = infinit, pentru orice i şi j
	next, matrice N x N în care vom salva prima muchie din drumul i-j de cost minim
	//next este necesar doar în cazul în care ne interesează muchiile folosite
//pasul k = 0
2. Pentru fiecare nod v
	1. dist[v][v] = 0;
3. Pentru fiecare pereche (u,v) a.i. există muchie de la u la v
	1. dist[u][v] = costMuchie(u,v);
	2. next[u][v] = v; //pentru urmărirea muchiilor ce compun drumul
//am terminat pasul k = 0
4. Pentru fiecare pas k (de la 1 la N)
	1. Pentru fiecare nod i (de la 1 la N)
		1. Pentru fiecare nod j (de la 1 la N)
			1. calculăm costul nou = dist[i][k] + dist[k][j];
			2. comparăm costul nou cu costul vechi = dist[i][j]
			 dacă e mai bun costul nou:
				1. dist[i][j] = costul nou;
				2. next[i][j] = next[i][k]; //pentru urmărirea muchiilor
			 altfel păstrăm costul vechi

Pentru obţinerea nodurilor ce formează drumul de cost minim de la u la v, putem folosi următoarea secvenţă:

funcţie afişareDrum(u, v)
1. dacă u == v
	1. print(v); STOP
2. print(u);
3. afişareDrum(next[u][v], v);

1. Daţi un exemplu de graf orientat cu un singur arc cu cost negativ pentru care algoritmul lui Dijkstra dă rezultate greşite.
2. Cum putem folosi algoritmul lui Dijkstra sau algoritmul Bellman-Ford pentru a obţine aceleaşi rezultate ca algoritmul Floyd-Warshall(drumul de cost minim pentru toate perechile de noduri)? Ne limităm la grafurile pe care merg toţi cei trei algoritmi.
3. Implementaţi unul din algoritmi pentru a calcula drumurile de cost minim de la un nod sursă la toate celelalte noduri într-un graf cu toate muchiile/arcele cu cost pozitiv.
4. Verificaţi dacă un graf conţine cicluri negative.

Pentru acest laborator puteți descărca scheletul de cod de aici. Descărcați arhiva și dezarhivați-o.

Puteti folosi utilitarul wget pentru descarcare si utilitarul unzip pentru dezarhivare.

• wget http://elf.cs.pub.ro/sda-ab/wiki/_media/laboratoare/lab7_drumuri_minime-skel.zip
• unzip lab7_drumuri_minime-skel.zip

Pentru compilare folositi comanda make. Pentru rulare puteti folosi comanda make run sau ./graph.

1. Se dă un graf pentru care se cunoaşte drumul de cost minim de la un nod sursă(S) la un nod destinaţie(D). Dacă adăugăm 100 la costul fiecărei muchii, se modifică drumul de cost minim? (dacă da, daţi un exemplu; dacă nu, explicaţi de ce).
2. Aceeaşi întrebare dacă înmulţim fiecare cost cu 100.
3. Cum găsiţi(mai rapid decât cu cei 3 algoritmi prezentaţi) drumul de cost minim de la S la D într-un graf în care toate muchiile au acelaşi cost(1)? Cum adaptaţi soluţia în cazul în care toate muchiile au costul 1 sau 2?
4. Daţi un exemplu în care folosirea algoritmului lui Dijkstra(pentru a obţine drumul de cost minim pentru toate perechile de noduri) ar fi mai rapidă decât algoritmul Floyd-Warshall.

1. Algoritmul lui Dijkstra
2. Algoritmul lui Bellman Ford
3. Algoritmul lui Floyd-Warshall
4. Protocoale de rutare