Sidebar
Table of Contents
Laborator 07: Operații pe numere lungi
Există situaţii excepţionale în care aspecte ale arhitecturii pe care lucrăm devin un impediment. Una dintre aceste situaţii este când problemele, pe care încercăm să le rezolvăm printr-un program pe calculator, au ca input numere foarte mari care nu pot fi reprezentate pe câte un singur registru. De exemplu pot exista cazuri în care datele citite de la tastatură să nu poată fi reprezentate pe registrele de 32 biţi (dacă suntem pe o arhitectură x86) sau pe 64 de biţi (dacă suntem pe o arhitectură amd64). În astfel de situaţii suntem nevoiţi să reprezentăm datele pe mai mulţi bytes decât ar putea procesorul în cauză să proceseze printr-o singură instrucţiune.
În acest laborator vom învăţa cum să facem calcule pe date care pot depăşi dimensiunea registrelor puse la dispoziţie de arhitectură.
Mindset
Reprezentarea numerelor
Numerele vor fi reprezentate ca multipli de operanzi care pot fi procesaţi de instrucţiunile procesorului.
În cazul arhitecturii x86 acest tip de operanzi pot fi: byte, word si double word.
Exemplu:
section .data a: db 0x11, 0x22, 0xAA, 0xBB, 0xCC ; , ... b: db 0x33, 0x44, 0xDD, 0xEE, 0xFF ; , ... r: resb 5
Primii bytes vor reprezenta cei mai puţini semnificativi bytes, în timp ce ultimii bytes vor reprezenta cei mai semnificativi bytes. În acest fel se respectă ordinea specifică arhitecturii x86 (little endian).
Dacă ar fi fost să reprezentăm aceste numere folosind words, declararea lor ar fi arătat astfel:
section .data a: dw 0x2211, 0xBBAA, 0xCC ; , ... b: dw 0x4433, 0xEEDD, 0xFF ; , ... r: resw 3
Observaţi diferenţa dintre primii doi bytes a lui a reprezentaţi cu db vs varianta în care sunt reprezentaţi cu dw.
Clasele primare
Fiecare număr este compus din mai mulţi operanzi de bază pe care procesorul poate efectua instrucţiuni efectiv. Toţi algoritmii care pot fi folosiţi pentru a efectua calcule pentru astfel de numere lungi se pot deduce dacă ne setăm ca mindset că vom trata fiecare tip operand de bază, care contribuie la compunerea unui număr mai mare, ca fiind o cifră din acel număr. Dacă considerăm numerele ca find reprezentate astfel, putem aborda algoritmii de bază din clasele primare din școala generală pentru a face operaţii de bază precum: adunare, scădere, înmulţire, împărţire, etc.
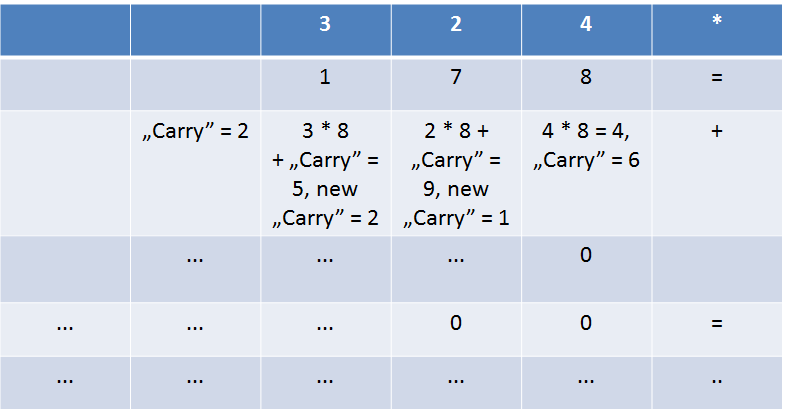
Exemplu mindset
În clasele primare, pe numere reprezentate în forma zecimală, foloseaţi un astfel de algoritm pentru a face adunarea între 2 numere care au cel puţin două cifre:
 Acum algoritmul adaptat pentru noi, unde fiecare cifră este un registru de 8 biți:
Acum algoritmul adaptat pentru noi, unde fiecare cifră este un registru de 8 biți:
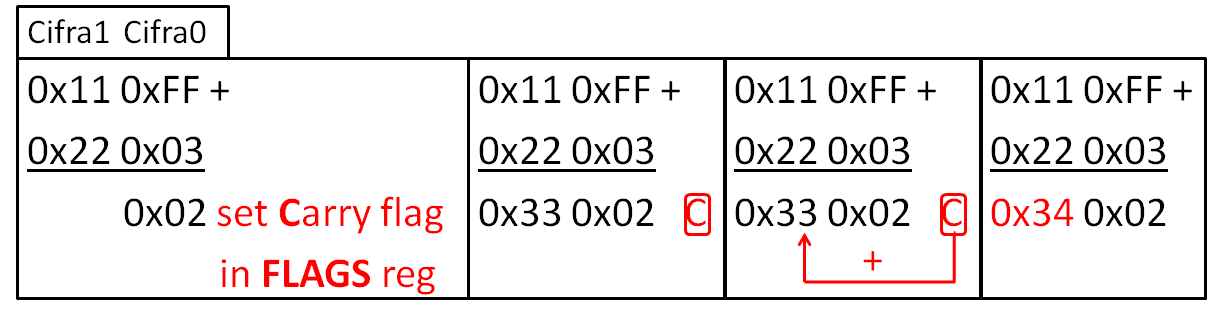
Adunare. Carry flag.
section .data str: db '%hu', 0 section .code ; ... ; add first two bytes mov al, byte [A_digit0] add al, byte [B_digit0] ; AL = A_digit0 + B_digit0 mov byte [result_digit0], al ; store the first digit of the result ; add, with Carry, the second two bytes mov al, byte [A_digit1] adc al, byte [B_digit1] ; AL = A_digit1 + B_digit1 + Carry mov byte [result_digit1], al ; store the second digit fo the result ; print number mov bl, [result_digit0] mov bh, [result_digit1] push bx push str call printf add esp, 6
În codul prezentat mai sus se adună prima cifră a fiecărui număr. Dacă cifra rezultatului depășește valoarea reprezentabilă în acel registru, atunci se activează bitul de Carry în registrul FLAGS. Apoi se face și adunarea celei de-a doua cifre din fiecare număr, la care se mai adaugă și Carry-ul (dacă este activat).
Adunare. Generalizare.
Un exemplu în care fiecare număr e reprezentat pe un vector mai lunguieț de operanzi de bază:
section .data A: db 0x11, 0x22, 0xAA, 0xBB, 0xCC B: db 0x33, 0x44, 0xDD, 0xEE, 0xFF len: dd $-b result: resb 5 section .code CMAIN: ; ... ; init loop resources: xor ecx, ecx ; ecx = 0 clc ; clear Carry flag; FLAGS[C] = 0 ; loop code: for: mov al, byte [A + ecx] ; get a digit from A adc al, byte [B + ecx] ; AL = A + B + Carry mov [result + ecx], al ; store result inc ecx cmp ecx, [len] ; end of for loop? jl for ; ...
În această variantă de cod se adună cifrele a două numere, luându-le byte cu byte. Pentru că la prima iterație nu știm în ce stare ne lasă flag-ul de Carry codul care s-a executat anterior, trebuie sa ne asigurăm ca acesta este setat pe 0 pentru ca rezultatul să fie corect.
Adunare. Optimizare.
Acum că am asigurat corectitudinea algoritmului, putem folosi puterea completă a arhitecturii. La varianta algoritmului în care folosim instrucțiuni cu registre de 8 biți, procesorul va avea de executat un număr mare de instrucțiuni (cel puțin câte o adunare pentru fiecare byte). Dacă trecem de la registre de 8 biți la registre de 32 de biți, calculul anterior se poate realiza în doar 2 add-uri, față de 5 din varianta inițială a algoritmului.
section .data A: dd 0xBBAA2211, 0xCC ; ... B: dd 0xFFEE4433, 0xFF ; ... len: dd ($-b)/4 result: resb 8 section .code CMAIN: ; ... ; init loop resources: xor ecx, ecx ; ecx = 0 clc ; clear Carry flag; FLAGS[C] = 0 ; loop code: for: mov eax, dword [A + ecx*4] ; get a digit from A adc eax, dword [B + ecx*4] ; AL = A + B + Carry mov [result + ecx*4], eax ; store result inc ecx cmp ecx, [len] ; end of for loop? jl for ; ...
Dacă încă foloseam varianta de declarare cu db am fi fost nevoiți să facem padding manual cu zero astfel încât a doua “cifră” a numărului să acopere un registru întreg. Dacă nu făceam padding, datele lui A ar fi intrat peste datele lui B.
Declararea corectă a lui A și B folosind db:
A: db 0x11, 0x22, 0xAA, 0xBB, 0xCC, 0, 0, 0 ; ... B: db 0x33, 0x44, 0xFF, 0xEE, 0xFF, 0, 0, 0 ; ...
Sign bit. Left padding.
După cum ştiţi, la numerele reprezentate în formă zecimală, se poate face padding în faţa numărului cu un set de cifre infinite de zero (de exemplu: 0000343 este fi acelaşi număr cu 343). Este perfect valabil şi la numerele reprezentate în binar, pot fi prefixate de oricâte cifre de zero (0010000100 este fix acelaşi număr ca 10000100).
Apare în schimb o situaţie dubioasă la numerele negative datorită felului în care sunt reprezentate în binar. Dacă vă mai aduceţi aminte, acestea se reprezintă în complement faţă de 2.
Înainte să vă zic un fact concret, haideţi să vedem cum evoluează reprezentarea numerelor negative la stânga, cu cât se apropie mai mult de zero:
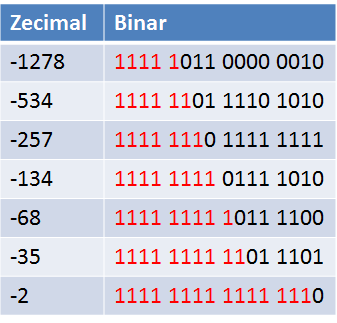
După cum se poate observa, și numerele negative au un padding la stânga (sau pot fi prefixate la stânga), dar cu cifre de 1.
Operații pe numere de lungimi diferite
Acum o să apară mici considerente când vom aduna numere de lungimi diferite:
- Dacă adunăm două numere negative, dacă se propagă un Carry care necesită un byte suplimentar, trebuie să ținem cont de acel padding de 1 în cazul reprezentării numerelor negative. Dacă se propagă pur și simplu un +1 numărul va fi interpretat ca un număr pozitiv (cea ce este greșit, nici măcar nu este activat bitul de semn în ultimul byte). Acest lucru este valabil și la numere negative de dimensiuni egale.
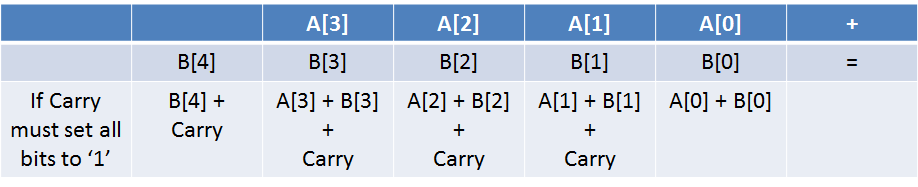
- “Last, but not least”: Dacă avem un număr pozitiv mai lung decât un număr negativ, și mai mare în modul, teoretic ar trebui să ne dea un număr mai mic. Dacă nu se face padding la stânga cu 1 astfel încât cele 2 numere să aibă lungime egală, s-ar putea să ne trezim cu un număr mai mare ca rezultat.
Demo practic:
; wrong representation for '-1' in A %include "io.inc" section .data A: db -1, 0 ; when loaded in register: 00000000 11111111 => will be seen as positive number B: dw 134 section .text global CMAIN CMAIN: mov ax, [A] add ax, [B] PRINT_DEC 2, ax ; will print 389 ret
; correct representation of '-1' in A %include "io.inc" section .data A: db -1, 0xFF ; when loaded in register: 11111111 11111111 B: dw 134 section .text global CMAIN CMAIN: mov ax, [A] add ax, [B] PRINT_DEC 2, ax ; will print 133 ret
- Ce se întâmplă dacă numerele au același semn? Dar dacă sunt de semn diferit?
- Dacă numerele sunt de lungime egală, dar de lungime diferită, mai ține algoritmul?
- Dacă combin elementele studiate mai sus, semn vs lungime, mai ține algoritmul meu?
- Ce se întâmplă dacă apare un Carry în timpul operației? Este ok dacă îl propag?
- Mai ține algoritmul dacă Carry-ul se propagă și la următorii 2-3 bytes?
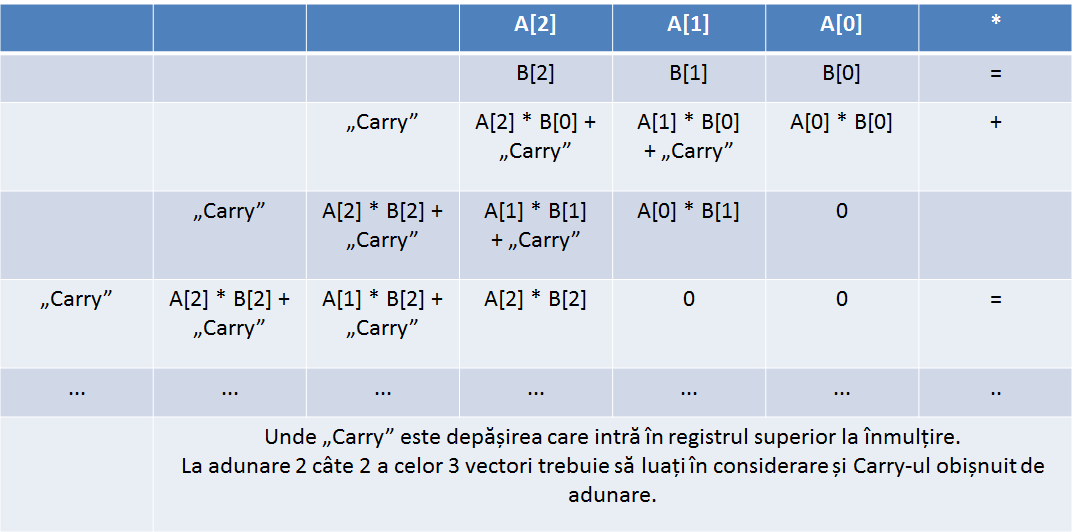
Înmulţiri
La înmulțiri nu avem un bit de Carry, pentru că operația de înmulțire crește mult mai repede decât o adunare. Însă, dacă vă mai aduceți aminte de la laboratoarele trecute, dacă pentru operația mul sunt folosiți operanzi de N biți, rezultatul va fi dat pe 2*N biți. Partea inferioară a numărului se va duce într-un registru something A something (EAX, AX sau AL), iar partea superioară (“Carry”-ul, commas intended) se va duce în alt registru (EDX, DX sau AH). În rest avem înmulțiri ca în clasele primare:
- varianta în care fiecare număr este reprezentat din mai mulți operanzi de bază cu care poate lucra procesorul (bytes, words, double words):
Împărţiri
Instrucțiunea de împărțire (div) folosește valorile a doi regiștri concatenați pe post de deîmpărțit.
Probabil mulți v-ați pus în cap: “Aș putea folosi…“

că ați putea folosi, de exemplu, registrele DX concatenat cu AX (DX:AX) pentru a împărți un număr de 32 de biți la 16 biți (sau, de ce nu, să împărțiți EDX:EAX la un operand de 32 de biți).
Să zicem ca am vrea să reprezentăm numărul 4444123 în DX:AX și că vrem să-l împărțim la 10 (care merge reprezentat și pe 16 biți). Ne-ar returna corect restul (=3), DAR ne-ar rămâne câtul 444412 care nu poate fi reprezentat, pentru că eventualul cât se depozitează în AX, care poate reține o valoare maximă de 65 536, AX fiind un registru de 16 biți.
Acestă reprezentare de la div ne ajută, dar pe post de “reverse” “Carry” de la înmulțire. Dacă ar fi fost să faceți împărțirea ca în clasele primare a operației menționate anterior, probabil ați fi făcut-o cam așa:
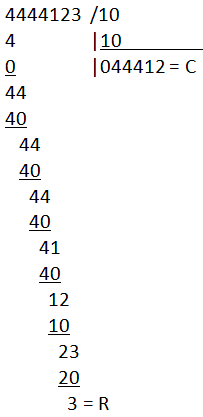
Haideți descriem toată operația sub o formă intermediară care să înceapă să semene cu div-ul nostru:
- Luăm prima parte din număr: 44 / 10 = 4 rest(“Carry”) 4
- A doua parte din număr: o să fie “Carry”:4 / 4 = iar 4 rest(“Carry”) 4 ; “Carry” concatenat cu 4 împărțit la 10 = 4 și un nou “Carry” tot de 4
- Reluat pasul anterior până când nu mai rămânem cu părți din număr pe care să le putem împărți
L-am segmenta în elemente de dimensiuni corespunzătoare operanzilor de bază ai arhitecturii (byte, word sau double word) și am itera prin ele în felul următor:
"Carry" = 0 // prepare/init "Carry"
for (i=0; i < length(nr); i++)
"Carry":[nr + i] / împărțitorul => "Carry" = rest, [nr + i] = cât
Shiftări
Prin operațiile de shiftare putem muta biți unui număr mai la stânga (instrucțiunea shl), sau mai la dreapta (instrucțiunea shr).
Biții care ies în afara numărului vor fi aruncați, mai puțin ultimul bit ieșit în afară. Acest ultim bit va ajunge în flagul Carry.
Spațiile libere lăsate în urma shiftării se vor completa cu biți de 0.
Left shift:

Right shift:

Aceste operații ne ajută să facem operații rapide cu puteri ale lui 2. Dacă vom shifta cu un bit un număr la stânga, acesta va arăta ca și cum ar fi fost înmulțit cu 2.
shl eax, 1; eax *= 2 shl eax, 2; eax *= 4 shl eax, 3; eax *= 8 ; etc.
Dacă shiftăm numărul cu o poziție la dreapta, acesta va arăta ca și cum ar fi fost împărțit la 2.
shr eax, 1; eax /= 2 shr eax, 2; eax /= 4 shr eax, 3; eax /= 8 ; etc.
Revenind la această informație:
Acest ultim bit va ajunge în flagul Carry.
Putem implementa shiftarea (înmulțirea și împărțirea cu puteri ale lui 2) pe numere reprezentate pe mai mulți operanzi de bază (bytes, words, double words) folosind flagul de Carry (avem instrucțiuni condiționale de tipul: jc si jnc (jump if [not] Carry)), și instrucțiuni logice de tipul AND şi OR.
Exerciții
[2p] 1. Împărţiri cu puteri ale lui 2
Implementaţi împărţirea unui număr cu puteri ale lui 2 fără a folosi instrucţiunea div. Datele de input ale programului vor fi: numărul deîmpărţit şi puterea la care se ridică 2.
[2p] 2. Increment flags
Următorul cod îşi propune să incrementeze un byte dintr-un număr, cât timp acesta nu se resetează la 0, folosind instrucţiuni pe operanzi de 8 biţi. După o rulare se poate observa însă ca programul nu se execută cu ne-am aştepta, mai exact rămâne în buclă infinită. Fără a modifica tipul operanzilor, corectaţi linia din loop care face incrementarea astfel încât programul să se termine şi la finalizarea lui să se afişeze 512.
- inc.asm
%include "io.inc" section .data nr: db 0x88, 0x1 section .text global CMAIN CMAIN: for: inc byte [nr] jnc for inc byte [nr + 1] PRINT_UDEC 2, nr xor eax, eax ret
[2p] 3. Înmulţirea corectă a 2 numere de lungimi diferite
Scrieţi o secvenţă de cod astfel încât să înmulţiţi nr1 cu nr2 şi să depuneţi rezultat în variabila result. Trebuie să folosiţi registre de 8 biţi.
- mul.asm
%include "io.inc" section .data nr1: dB 0x90, 0x02 ; =656 nr2: dB 0x04 result: dw 0 section .text global CMAIN CMAIN: ; TODO multiply nr1 by nr2 using only 8bit registers ; store the result in the "result" variable PRINT_UDEC 2, result ; should be 2624 xor eax, eax ret
[2p] 4. Suma elementelor (fără semn) ale unui vector
Pornind de la scheletul de cod următor, implementaţi suma elementelor ale unui vector folosind registre de 8 biţi (obligatoriu):
- sum.asm
%include "io.inc" section .data v: dB 12, 56, 93, 44, 55, 23, 44, 71, 43 len: dd $-v sum: dW 0 section .text global CMAIN CMAIN: ; TODO sum vector of BYTE elements into "sum" WORD variable PRINT_UDEC 2, sum ; should be 441 if result is correct xor eax, eax ret
[2p] 5. Înmulţirea cu 2 a unui număr mare/lung
Implementaţi înmulţirea unui număr cu 2, fără a folosi instrucţiunea mul.
- Numărul trebuie să aibă cel puţin 5 bytes în alcătuirea sa.
- Trebuie să folosiţi instrucţiunea OR.
[1p] 6. BONUS: Suma elementelor (cu semn) ale unui vector
Pornind de la scheletul de cod următor, implementaţi suma elementelor (cu semn) ale unui vector folosind registre de 8 biţi (obligatoriu):
- signed_sum.asm
%include "io.inc" section .data v: dB 12, -56, 93, 44, 55, -23, 44, 71, 43 len: dd $-v sum: dW 0 section .text global CMAIN CMAIN: ; TODO sum vector of BYTE elements into "sum" WORD variable PRINT_UDEC 2, sum ; should be 283 if result is correct xor eax, eax ret
[1p] 7. BONUS: Împărţirea a 2 numere de lungimi diferite
Realizaţi împărţirea corectă a lui nr1 la nr2 folosind registre de maxim 16 biţi:
- div.asm
%include "io.inc" section .data nr1: dd 4444123 nr2: dw 10 result: dd 0 section .text global CMAIN CMAIN: ; TODO divide nr1 by nr2 ; by using registers of size up to 16 bits and ; store the result in the "result" variable PRINT_UDEC 4, result ; should be 444412 xor eax, eax ret
[1p] 8. BONUS: Îmbunătăţire înmulţiri cu 2
Observaţi şi utilizaţi instrucţiunile de rotire cu Carry, în locul celor de tip AND si OR, pentru a rezolva exerciţiului 5.
[1p] 9. BONUS: Generalizare înmulţiri cu puteri ale lui 2
Modificaţi exerciţiul 5 astfel încât numărul să se poată înmulţi cu o variaţie mai mare de puteri ale lui 2 (cu aceleaşi limitări ca la 5).