Sidebar
Table of Contents
Laborator 01: Introducere
Pentru reprezentarea informațiilor (instrucțiuni și date), calculatoarele folosesc sistemul binar (baza 2). În cazul scrierii programelor în limbaj de asamblare este preferat sistemul hexazecimal (baza 16), pentru că scutește programatorul de scrierea șirurilor lungi de 1 și 0, iar conversia din/în binar se poate face mult mai ușor decât în cazul sistemului zecimal (baza 10).
Să presupunem următoarea instrucțiune în limbajul C:
char a = 113;
Această instrucțiune are ca efect stocarea în memorie a unui octet cu valoarea 113, care va fi reprezentat în forma binară: 0b01110001. Aceeași valoare poate fi scrisă în hexazecimal ca 0x71.
Sistemele binar și hexazecimal
Înainte de a începe lucrul cu limbajul de asamblare, este necesar să ne familiarizăm cu sistemele binar și hexazecimal și cu modalitățile de conversie între ele.
În sistemul binar (baza 2), valorile sunt reprezentate ca un șir de 0 și 1. Fiecare cifră din șir reprezintă un bit, iar un grup de 8 biți formează un octet (byte). Un grup de 4 biți poartă denumirea de nibble, sau half-byte.
În sistemul hexazecimal (baza 16), valorile sunt reprezentate sub forma unui șir de caractere din intervalul '0'-'9' sau 'a'-'f'. Un octet este format din două astfel de caractere, deci fiecare caracter corespunde unui grup de 4 biți (un nibble).
Conversia din zecimal în binar/hexazecimal
- Se împarte succesiv numărul la numărul bazei (2 sau 16) și se rețin resturile
- Când câtul împărțirii devine 0, se scriu resturile în ordine inversă.
- În cazul bazei 16, atunci când restul este mai mare decât 9 se folosesc literele a-f (10=a, 15=f)
Exemplu: conversia numărului 113 în hexazecimal
- Pas 1: 113/16 = 7, rest 1
- Pas 2: 7 / 16 = 0, rest 7
- Câtul este 0, deci putem obține numărul în hexazecimal scriind resturile în ordine inversă: 0x71
Conversia din binar/hexazecimal în zecimal
Un număr convertit din baza X în baza 10 are valoarea egală cu suma produselor dintre fiecare cifră din numărul în baza X și X la puterea egală cu poziția cifrei în numărul respectiv (numărarea se face de la dreapta la stânga, începând cu 0).
Exemplu: conversia numărului 0xD9B1 în zecimal
0xD9B1 = 1*160 + 11*161 + 9*162 + 13*163 = 55729
Conversia intre binar și hexazecimal
După cum am precizat anterior, o cifră din cadrul unui număr în hexazecimal corespunde unui grup de 4 biți (un nibble). Astfel, pentru a converti un număr din hexazecimal în binar este suficient să transformăm fiecare cifră în grupul de 4 biți echivalent.
Exemplu: Conversia numărului 0xD9B1 în binar
- 0x1 = 0b0001
- 0xB = 0b1011
- 0x9 = 0b1001
- 0xD = 0b1101
Astfel, numărul obținut în binar este 0b1101100110110001.
Operația inversă, conversia din binar în hexazecimal se poate face convertind fiecare grup de 4 biți în cifra corespunzătoare în hexazecimal.
Reprezentarea numerelor
În memoria unui calculator o valoare este memorată pe un număr fix de biți. Dimensiunea cuvântului (word size) arhitecturii unui procesor reprezintă numărul maxim de biți cu care procesorul îi poate accesa printr-o singură operație.
Dimensiunile tipurilor de date uzuale folosite în C sunt dependente atât de procesor, cât și de platforma cu ajutorul căreia a fost compilat programul (sistem de operare, compilator). În tabelul de mai jos sunt prezentate dimensiunile tipurilor de date pe un procesor cu dimensiunea cuvântului arhitecturii de 32 de biți, în cazul în care programul este compilat folosind gcc, sub Linux.
| Tip de date | Număr biți | Număr octeți |
|---|---|---|
| char | 8 | 1 |
| short | 16 | 2 |
| int | 32 | 4 |
| long | 32 | 4 |
| long long | 64 | 8 |
| pointer | 32 | 4 |
Integer overflow
În cazul în care un număr trebuie reprezentat în binar pe un număr de biți mai mare decât numărul maxim alocat, atunci vor fi păstrați doar biții care încap (începând din partea dreaptă), iar restul sunt ignorați. Această situație poartă denumirea de integer overflow.
Un overflow poate să apară și în cazul în care se efectuează o operație (de exemplu adunare), iar rezultatul se dorește să fie reprezentat pe același număr de biți ca și operanzii. În acest caz este posibil ca rezultatul să nu încapă pe numărul respectiv de biți, iar primul bit (din stânga) să fie ignorat. O soluție folosită în procesoare pentru această situație este memorarea separată a unui bit în cazul în care operația duce la integer overflow, numit bit de depășire (carry bit).
Exemplu de integer overflow la adunare
Să presupunem că dorim să adunăm două valori stocate pe un octet, iar rezultatul să fie memorat tot pe un octet.
O1 = 171 = 0b10101011 O2 = 113 = 0b01110001 Rezultatul așteptat: 171+113 = 0b100011100 Rezultatul memorat pe 8 biți: 0b00011100 Carry bit = 1
Numere cu semn și fără semn
Folosind N biți putem memora 2N valori, de exemplu între 0 și 2N-1. Aceste valori sunt fără semn (toate sunt pozitive), pentru că nu putem face deosebirea între cele pozitive și negative. Dacă dorim și reprezentarea valorilor negative, trebuie să alocăm o parte din combinațiile binare posibile pe N biți pentru aceste valori.
În practică se împart combinațiile posibile astfel:
- prima jumătate este folosită pentru numere pozitive între 0 și 2N-1-1.
- a doua jumătate este alocată numerelor negative, între -2N-1 și -1.
De exemplu, pentru valori reprezentate pe 8 biți, împărțirea se face astfel:
- combinațiile binare între 0b00000000 și 0b011111111 corespund valorilor între 0 și 127.
- combinațiile între 0b10000000 și 0b11111111 corespund valorilor între -128 și -1 (0b10000000=-128, 0b11111111=-1).
Această reprezentare a fost aleasă pentru că prezintă o serie de avantaje:
- Putem determina foarte ușor dacă un număr este negativ sau pozitiv, după valoarea primului bit (1=negativ, 0=pozitiv)
- Pentru numere pozitive avem aceeași reprezentare ca în cazul numerelor fără semn.
- Operațiile aritmetice se fac exact ca în cazul numerelor fără semn
Pentru negarea unui număr (transformarea în complement față de 2) se procedează astfel:
- Se neagă toți biții din reprezentarea numărului în baza 2
- Se adună valoarea 1.
Exemplu: Reprezentarea valorii -29 în binar
- 29 = 0b00011101.
- Valoarea negată: 0b11100010.
- -29 = 0b11100010 + 1 = 0b11100011
Ordinea de reprezentare a numerelor mai mari de un octet (Little-Endian vs Big-Endian)
Pentru reprezentarea valorilor mai mari de un octet există două metode posibile, ambele folosite în practică:
- Little-Endian: cel mai puțin semnificativ octet este memorat primul (octeții sunt memorații în ordine inversă). Acest model este folosit de familia de procesoare Intel x86.
- Big-Endian: cel mai semnificativ octet este memorat primul.
Exemplu: Dorim să stocăm valoarea 0x4a912480 în memorie pe 32 de biți (4 octeți), începând cu adresa 0x100, folosind cele două metode:
| Metoda | Adresa 0x100 | Adresa 0x101 | Adresa 0x102 | Adresa 0x103 |
|---|---|---|---|---|
| Little-Endian | 0x80 | 0x24 | 0x91 | 0x4a |
| Big-Endian | 0x4a | 0x91 | 0x24 | 0x80 |
Avantaje Little-Endian
1. Valorile mici (pe un octet) sunt stocate mereu la aceeași adresă, indiferent de dimensiunea tipului de date folosit.
Exemplu: Dorim stocarea valorii 0x49 la adresa 0x2000 cu tipurile char, short și int:
| Tip de date | 0x2000 | 0x2001 | 0x2002 | 0x2003 |
|---|---|---|---|---|
| char | 0x49 | - | - | - |
| short | 0x49 | 0x00 | - | - |
| int | 0x49 | 0x00 | 0x00 | 0x00 |
2. Oferă ușurință în efectuarea operațiilor aritmetice. Majoritatea operațiilor se efectuează începând cu cel mai puțin semnificativ octet, iar acesta este stocat primul în cadrul acestui mod de reprezentare, deci putem efectua operațiile pe mai mulți octeți parcurgând operanzii de la adresa cea mai mică adresă la cea mai mare.
Avantaje Big-Endian
1. Valorile nu necesită transformări în momentul în care se transmit pe rețea. Pentru a se putea realiza comunicația între două calculatoare care folosesc metode diferite de reprezentare, toate valorile transmise sunt reprezentate în formatul Network byte order, care este echivalent cu Big-Endian.
2. Valorile pe mai mulți octeți sunt mai ușor de citit în momentul examinării unei zone de memorie.
Operații cu valori reprezentate în binar
Operații aritmetice
Operații logice
Operatori pe valori binare
- Inversare (NOT): se inversează fiecare bit. Exemplu: INV(0b10011010) = 0b01100101
- Și logic (AND): se efectuează operația 'și' între biții de pe aceleași poziții din operanzi. Exemplu: 0b1001 AND 0b0111 = 0b0001
- Sau logic (OR): se efectuează operația 'sau' între biții de pe aceleași poziții din operanzi. Exemplu: 0b1001 OR 0b0111 = 0b1111
- Sau exclusiv (XOR): dacă biții de pe aceleași poziții din operanzi au valori egale, bitul rezultat are valoarea 0, altfel are valoarea 1. Exemplu: 0b1001 XOR 0b0111 = 0b1110
Deplasări (Shifts)
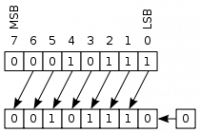
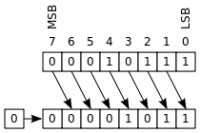
Deplasări logice
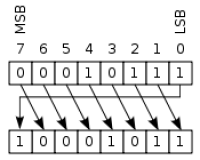
Deplasările logice dreapta/stânga presupun mutarea cu o poziție a fiecărui bit. Cum rezultatul trebuie să fie pe același număr de biți ca valoarea inițială, primul bit este pierdut, iar spațiul gol este completat cu bitul 0.
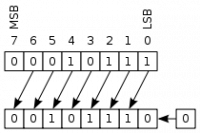
Deplasări aritmetice
Deplasarea aritmetică stânga este identică cu cea logică. În schimb, deplasarea aritmetică dreapta păstrează semnul valorii (în cazul în care primul bit este 1, deci numărul este negativ, rezultatul trebuie să fie tot negativ).
Similar, deplasarea unei valori cu N poziții la dreapta este echivalentă cu împărțirea valorii respective la 2N (și rotunjirea rezultatului la partea întreagă).
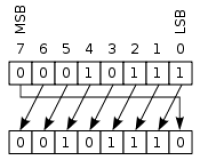
Rotații
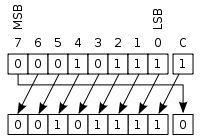
Operația de rotire (numită și deplasare circulară) este similară cu cea de deplasare, singura diferență fiind aceea că spațiul gol generat de deplasare este înlocuit cu bitul eliminat.
Majoritatea procesoarelor permit un tip special de rotire, și anume rotire folosind un bit auxiliar. De obicei, ca bit auxiliar se folosește bitul de carry. În acest caz, spațiul gol este înlocuit cu bitul auxiliar, iar bitul eliminat este memorat în acest bit.
Exerciții
1. (4p) Efectuați următoarele conversii între sisteme de numerație:
a. Din decimal în binar și hexazecimal:
- 58
- 121
- 18446
b. Convertiți în zecimal:
- 0b11000
- 0b1011
- 0b1100010111010010
- 0xD8
- 0x7A
- 0xBB29
c. Din hexazecimal în binar:
- 0x5e
- 0x4A01
- 0x0941D583
d. Din binar în hexazecimal:
- 0b01111101
- 0b1000110000011111
- 0b1111101011101011
2. (1p) Aflați dimensiunile principalelor tipuri de date din C pe sistemele din laborator. (char, short, int, unsigned int, long, long long, pointer). Hint: sizeof.
3. (1p) xxd este un utilitar Linux ce permite afișarea fișierelor binare în diferite formate. Puteți găsi o versiune pentru Windows aici: xxd.zip.
Se dă fișierul binar din arhiva următoare: binary_file.zip. Să se afișeze folosind xxd conținutul acestui fișier în următoarele formate:
- ASCII (ca text) - nu trebuie să folosiți xxd.
- binar
- hexazecimal
4. (1p) Scrieți un program C cu ajutorul căruia să afișați următorul șir hexazecimal ca text: 48455820526f636b73210a.
Hint 2: În C puteți folosi codurile în format hexazecimal în locul caracterelor ASCII în șiruri de caractere cu ajutorul prefixului \x. Exemplu: char a[] = “\x41\x42\x43”; este echivalent cu char a[] = “ABC”; (puteți vedea aici un tabel cu codurile caracterelor ASCII)
5. (1p) Se dau următoarele declarații de variabile în C:
#include <stdio.h> void main() { unsigned int a = 4127; int b = -27714; unsigned long c = 0x12345678; char d[] = {'I', 'O', 'C', 'L', 'A'}; // TODO }
Observați cum sunt memorate aceste variabile în memorie.
6. (1p) Afișați valorile variabilelor c, d și e din programul de mai jos și explicați rezultatele (puteți converti valorile în binar pentru a observa mai ușor cauzele):
#include <stdio.h> void main() { short a = 20000; short b = 14000; short c = a + b; unsigned short d = 3 * a + b; short e = a << 1; // TODO }
7. (1p) Scrieți un program C cu ajutorul căruia să efectuați operația XOR între următoarele șiruri haxazecimale (octet cu octet) și afișați rezultatul ca text (hint: operatorul ^):
- 4c26e3b44c86c21ef8908970c7af7475c17e834c7c01aa702e77
- 004382c622a6b671d8e5fa15e7c7110de107ec395c6cdf035a56