User Tools
Sidebar
Table of Contents
Strategy definition
$\hat{s}_A(\hat{h}) = s_A(h) $ (or equivalently $=s_A(last(\hat{h}))$).
Some examples
In the induction step of $\langle B \rangle \varphi$ where $\varphi$ contains cooperation modalities, we want to replace each outermost occurrence of $\xi = \langle A \rangle \gamma$ in $\varphi$ by a proposition $p_\xi$.
For simplicity, suppose we only have one such occurrence $\xi$.
We also need to modify the model $M$ to $M^\xi$, such that:
the original formula holds in $M$ iff the transformed one holds in $M^\xi$.
We schematically illustrate four such transformations on models.
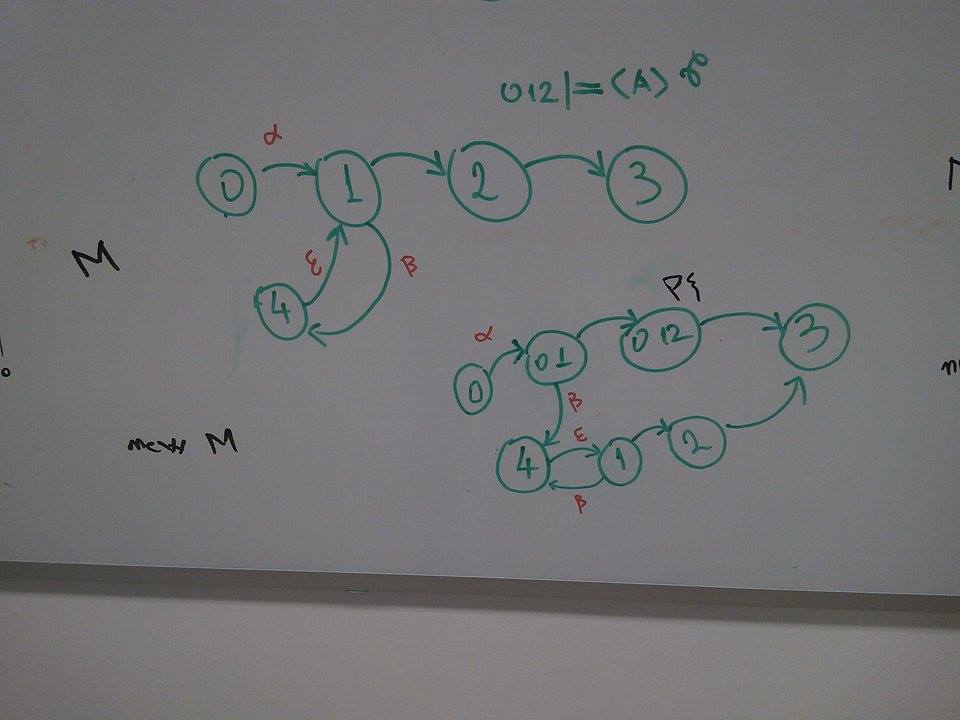
Example 1
In $M$, $\alpha$ is an action profile (action profiles are not illustrated if they are not important).
Suppose $012\models \langle A \rangle p$. In the transformed model, we label state $012$ by $p_\xi$.
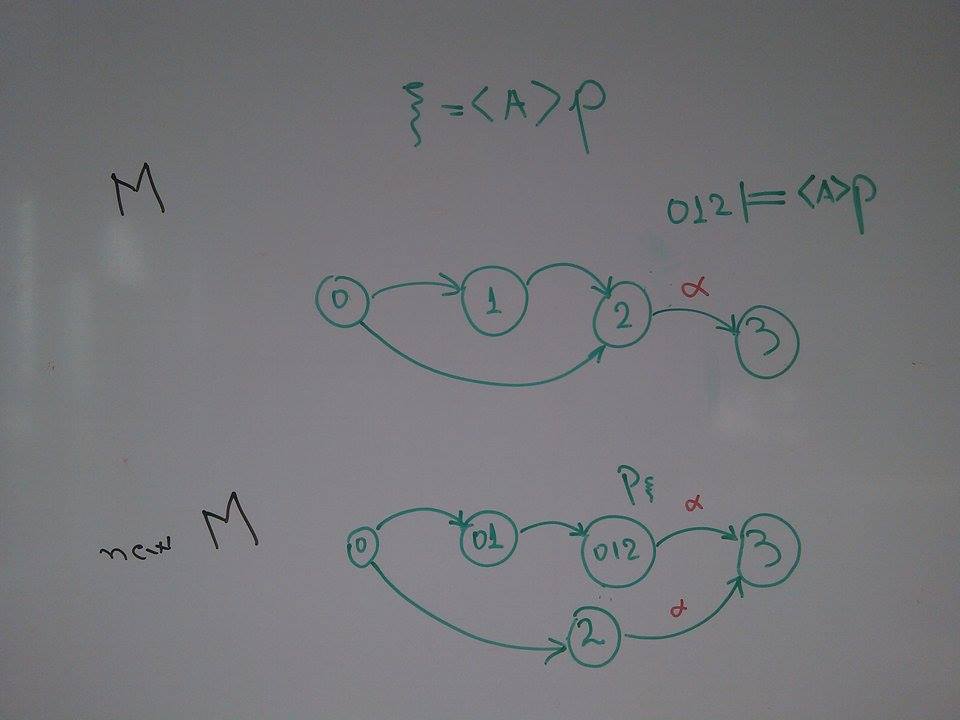
Example 2
In $M$, $\xi=\langle A \rangle G a$. We have $012^+ \models \xi$. In the transformed model, we have an infinite number of states, each one corresponding to a history $012..2$. They are all labelled with $p_\xi$.
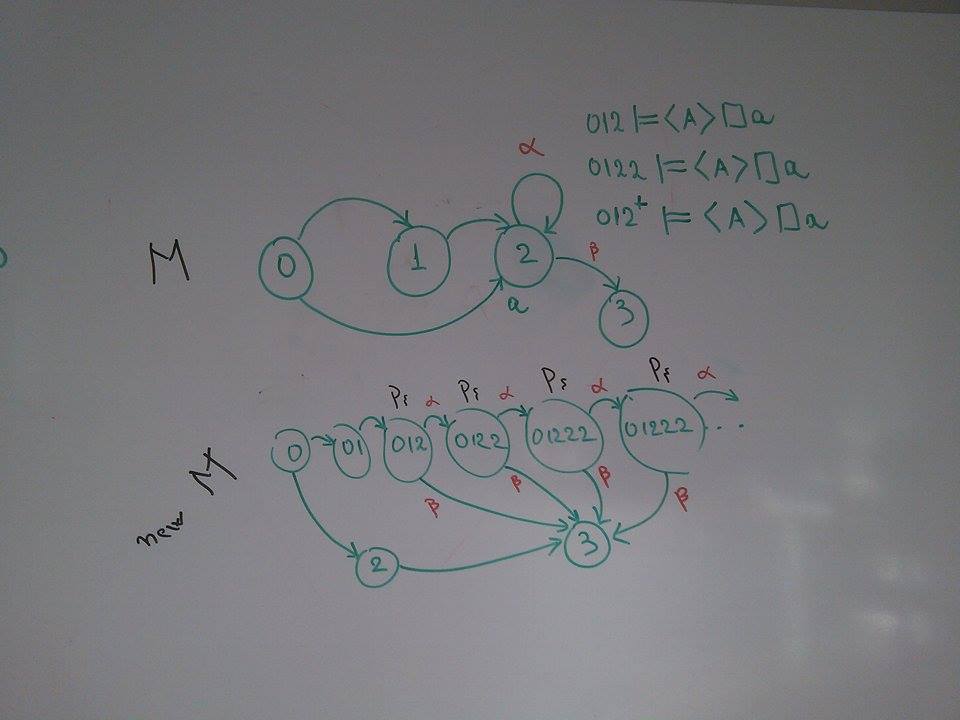
Example 3
The model $M$ shows that, in some situations, we may need to create states which do not correspond to histories per se.
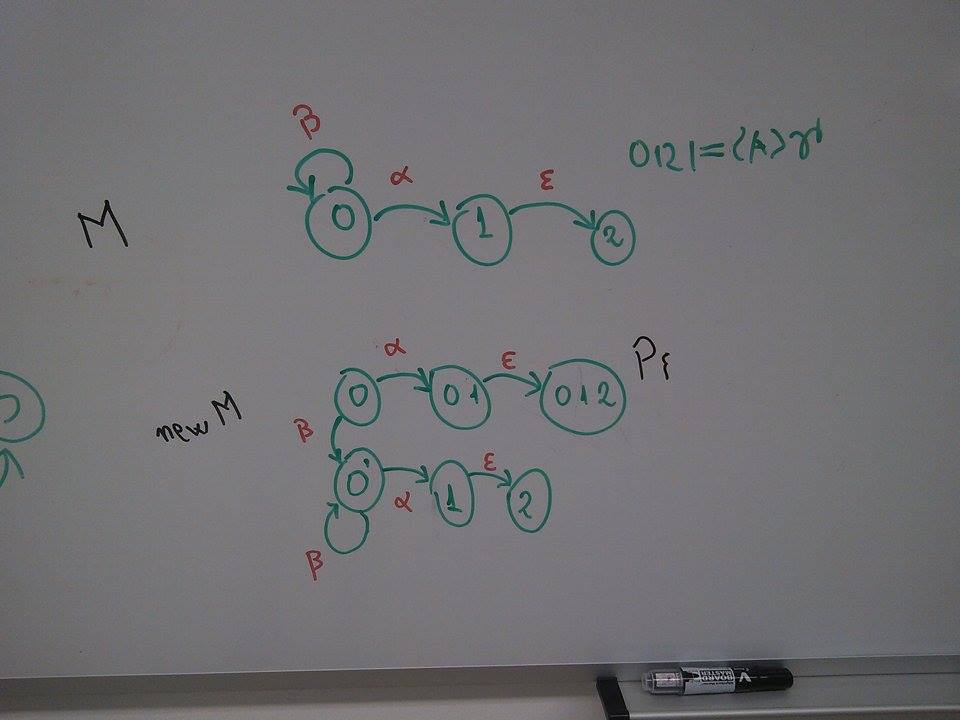
Example 4
Fixing tree proofs
Let $(M,q)$ be an iCGS and fix $h\in\Lambda_M(q)$. Let $\xi=\langle A'\rangle \gamma'$ be an ATL formula where $\gamma'$ does not contain cooperation modalities. We construct the model $(M^{\xi},q)$ w.r.t. $(M,q)$, $\xi$ and $h$, as follows:
- Let $h'=hh''$ (i.e. $h'$ extends $h$ by some history) be a history such that $M,h'\models \xi$.
- We remove from $M$ all states $q = h''[i]$ (i.e. all states from the extension $h''$)
- For each $h^*$ such that:
- $h^*$ extends $h$
- $last(h^*) = last(h')$
- create a unique state $h^*$ in $M^\xi$. Each such state corresponds to a “road” starting with $h$ and leading to the “point” where $\xi$ holds.
- add transitions exactly as in the unfolding.
- add indistinguishability relations as in the unfolding.
- Label this state $h^*$ with all propositions in $last(h^*)$. Additionally, if $h^*=h'$, label it with $p_\xi$.
- This process is repeated for each $h'$, and “duplicate” states $h^*$ can be “merged”
The construction $M^{\xi}$ partially unfolds $M$, and creates unique states for all histories starting with $h$, and ending with $last(h')$, for all $h'$ satisfying the above condition.
Lemma 1 Fix $h$. $M,hh''\models \xi \iff M^{\xi},h\hat{h''}\models p_\xi$, where $\hat{h''} = h''[0]h''[0,1]h''[0,2]\ldots h''$. The proof is similar to the base case $\varphi = \langle A\rangle \gamma$ from the paper.
We recursively define $M^{\{\xi_1,\ldots,\xi_k\}}$ as $(M^{\xi_1})^{\{\xi_2,\ldots,\xi_k\}}$.
Lemma 2 Fix h and $X=\{\xi_1\ldots,\xi_k\}$. For all $\xi_i$:
$M,hh''\models {\xi_i} \iff M^X,h\hat{h''} \models p_{\xi_i}$
Fixing the proof of Proposition 5.4.
In the induction step, instead of transforming $M$ by relabelling states, we transform $M$ to $M^{X}$ where $X$ contains the outermost occurrences of cooperation modalities in $\gamma$. In the resulting model, these formulae hold in exactly the same partially-unfolded histories, so we can apply the induction step.
Old stuff (10 May)
Proof sample of Prop. 5.4. (case $\star$).
$M,h\circ\lambda, k \models \varphi$ iff $T,\hat{h}\circ\hat{\lambda},k\models \varphi$.
Case $\varphi = \langle A \rangle \gamma$ where $\gamma$ contains cooperation modalities. Let $\xi$ designate an arbitrary occurrence of $\langle A' \rangle \gamma'$ in $\gamma$. (for example $\varphi = \langle A \rangle F(p \wedge \langle A' \rangle\gamma')$).
For each $h'$ such that:
- $|h'| = k' \geq k$,
- $h'[0,k] = h$,
- $M,h' \circ \lambda',k' \models \xi$
we perform the following relabelings:
- for each $k \leq i< k'$: relabel each $h'[0,i]\in T$ and $last(h'[0,i])\in M$ with a new proposition $p^{h'}_\xi$.
- relabel $h'\in T$ and $last(h)\in M$ with a new proposition $q^{h'}_\xi$.
We perform the following transformations on the formula $\varphi$: (unclear in the general case).
- For example, $\langle A\rangle F (x \wedge \langle B \rangle\gamma)$ is transformed to:
- $\langle A\rangle p_\xi \mathcal{U} (x \wedge q_\xi)$
- For example, $\langle A\rangle G (x \wedge \langle B \rangle\gamma)$ is transformed to: ?!?!
IGNORE BELOW - Proof (9th May)
Proof sample of Prop. 5.4. (case $\star$).
$M,h\circ\lambda, k \models \varphi$ iff $T,\hat{h}\circ\hat{\lambda},k\models \varphi$.
Case $\varphi = \langle A \rangle \gamma$ where $\gamma$ contains cooperation modalities. Let $\xi$ designate an arbitrary occurrence of $\langle A' \rangle \gamma'$ in $\gamma$. (for example $\varphi = \langle A \rangle F(p \wedge \langle A' \rangle\gamma')$).
For each $h'$ such that:
- $|h'| = k' \geq k$,
- $h'[0,k] = h$,
- $M,h' \circ \lambda',k' \models \langle A' \rangle\gamma'$
we relabel $h'\in T$ and $last(h')\in M$ with a new proposition $p_\xi$.