• Responsabil: Mihaela Pînzaru Diana Despa Cosmin Petrişor
• Deadline: 1.11.2015, 23:55
• Data publicării: 19.10.2015, 00:00
• Data ultimei modificări: 25.10.2015, 12:06
• Data tester-ului: 25.10.2015, 11:30

• Familiarizarea cu limbajul Java
• Dezvoltarea abilităţilor de bază de organizare a surselor şi controlul accesului
• Utilizarea unui design orientat-obiect şi exploatarea conceptului de încapsulare
• Respectarea unui coding-style adecvat

Francis şi Claire, două dintre cele mai populare şi influente persoane publice ale momentului, sunt mereu preocupate de opinia publică. Având în vedere faptul că astăzi cele mai multe informaţii sunt împărtăşite de persoane din toate colţurile globului prin intermediul reţelelor sociale, Francis şi Claire manifestă un interes special pentru acest mod de interacţiune.

Pentru a înţelege cât mai bine modelul şi funcţionalitatea unei astfel de reţele, cei doi s-au gândit să ceară consultanţă studenţilor de la Automatică şi Calculatoare. Cum cel mai bun mod de a explica un concept este printr-un exemplu practic, sarcina voastră fiind să implementaţi o reţea socială cu un model simplificat, dar din care să poată fi extrase informaţii relevante.

Vom descrie o reţea socială cu ajutorul unui graf neorientat. Nodurile grafului vor reprezenta utilizatorii, iar muchiile vor descrie relaţiile dintre aceştia. Astfel, va exista o muchie între oricare două noduri dacă şi numai dacă utilizatorii reprezentaţi de cele două noduri sunt prieteni.

Putem exprima această condiţie şi într-un mod formal:

               ∀ u, v ∈ V(G), (u, v) ∈ E(G) ⇔ prieteni(u, v) = True
                 V - mulţimea nodurilor din G
                 E - mulţimea muchiilor din G

Aşa cum am învăţat din primele laboratoare ne vom folosi de conceptul de încapsulare pentru a stoca şi manipula datele într-un mod cât mai simplu şi transparent.

Acestea fiind spuse vom modela utilizatorii reţelei cu ajutorul unei clase User, ce va conţine următoarele informaţii:

• ID: număr întreg pozitiv
• Nume: şir de caractere
• Prieteni: structură de date ce va conţine obiecte de tip User, ordonate crescător după ID

Reţeaua propriu-zisă va fi o clasă separată, Network, ce va menţine informaţii despre utilizatorii înregistraţi:

• Utilizatori: structură de date ce va conţine obiecte de tip User, de asemenea ordonate crescător după ID

Din descrierea de mai sus a claselor putem deduce faptul că reprezentarea grafului reţelei se va face prin intermediul listelor de adiacenţă. Vom folosi această abordare pentru a simplifica implementarea şi pentru a nu impune regula ca ID-urile utilizatorilor să fie neapărat numere naturale consecutive.

Prima voastră sarcină este să implementaţi funcţionalităţile de bază ale reţelei sociale: adăugarea / ştergerea unui utilizator, adăugarea / ştergerea unei relaţii de prietenie între doi utilizatori, etc.

Pentru a realiza acţiunile enumerate mai sus, reţeaua va trebui să accepte următoarele comenzi:

• ADD <ID> <Nume>
  • Comanda va crea un utilizator nou cu id-ul ID şi numele Nume, pe care îl va înregistra în graful reţelei.
  • Dacă utilizatorul a fost înregistrat cu succes comanda va afişa textul OK. În cazul în care există deja un utilizator înregistrat, cu acelaşi id, comanda va afişa DUPLICATE.
• REMOVE <ID>
  • Această comandă va elimina utiliziatorul cu id-ul ID din graful reţelei.
  • Dacă operaţia s-a desfăşurat cu succes se va afişa textul OK. În cazul în care nu există un utilizator înregistrat cu id-ul ID se va afişa textul INEXISTENT.
• FRIEND <ID1> <ID2>
  • Comanda va adăga o muchie în graful reţelei între nodurile reprezentate de utilizatorii cu id-urile ID1 şi ID2, ce va reprezenta relaţia de prietenie dintre aceştia.
  • Dacă operaţia s-a desfăşurat cu succes se va afişa textul OK. De asemenea, se va afişa OK şi dacă cei doi utilizatori erau deja prieteni. În cazul în care unul dintre cei doi utilizatori nu este înregistrat în graful reţelei (sau ambii) se va afişa textul INEXISTENT.
• UNFRIEND <ID1> <ID2>
  • Această comandă reprezintă inversul comenzii FRIEND, eliminând muchia dintre utilizatorii cu id-urile ID1 şi ID2.
  • De asemenea, dacă operaţia a avut loc cu succes se va afişa textul OK, iar în caz contrar INEXISTENT. Chiar dacă ambii utilizatori sunt înregistraţi, dar nu sunt prieteni, se va considera că operaţia eşuează.
• PRINT <ARG1> <ARG2> …
  • Comanda va primi un număr variabil de parametrii, în funcţie de informaţiile cerute.
  1. USER <ID>
     • Va afişa informaţii despre utilizatorul cu id-ul ID, în formatul:
       

       ID Nume: ID_FRIEND1 ID_FRIEND2 ...

     • ID_FRIEND1 ID_FRIEND2 … reprezintă lista de id-uri ale prietenilor utilizatorului asupra căruia se aplică comanda PRINT. Dacă utilizatorul cu id-ul ID nu există, va fi afişat textul INEXISTENT.
  2. NETWORK
     • Va afişa întreg graful reţelei de socializare.
     • Formatul de afişare va fi următorul:
       

       ID1 Nume_User1: ID_FRIEND1 ID_FRIEND2 ...
       ID2 Nume_User2: ID_FRIEND1 ID_FRIEND2 ...
       ...

  3. COMMUNITIES
     • Vezi Task 2 - Comunităţi.
  4. STRENGTH <ID>
     • Vezi Task 3 - Gradul de socializare.

Acum că avem la dispoziţie o reţea socială funcţională ne dorim să extragem informaţii cât mai relevante despre modul în care interacţionează utilizatorii acesteia. Astfel, ne propunem să identificăm, pe baza topologiei grafului, toate comunităţile existente în reţea.

Definim o comunitate ca fiind o componentă conexă a grafului reţelei. O componentă conexă a unui graf neorientat G este reprezentată de un subgraf S cu următoarele proprietăţi:

• ∀ u, v ∈ S, există un drum de la u la v (implicit şi de la v la u);
• ∀ u ∈ S, ∀ k ∈ (G - S), nu există un drum de la u la k (sau invers).

Mai pe scurt, o comunitate este formată dintr-un grup de utilizatori izolaţi ai reţelei.

Pentru a obţine informaţii despre comunităţile existente vom adăuga funcţionalitate comenzii PRINT descrisă anterior. Aceasta va fi apelată cu parametrul:

• COMMUNITIES
  • Va afişa componentele conexe ale grafului reţelei, în ordinea descoperirii lor cu un algoritm de parcurgere în adâncime.
  • Formatul de afişare va fi următorul:
    

    SIZE1: ID1 ID2 ...
    SIZE2: ID1 ID2 ...
    ...

  • SIZE1 SIZE2 … reprezintă dimensiunile comunităţilor, iar ID1 ID2 … reprezintă lista de id-uri ale utilizatorilor ce fac parte din comunitatea în cauză.
  • Atenţie: id-urile vor fi afişate în ordinea descoperirii (s-ar putea să nu fie neapărat în ordine crescătoare).

În graful din imagine am abstractizat utilizatorii prin noduri, notând doar id-urile acestora.

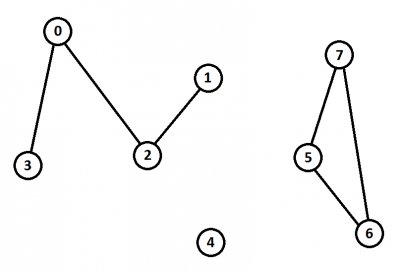
În urma parcurgerii în adâncime (DFS), plecând din nodul 0, vom descoperi componenta conexă (0, 2, 1, 3), apoi, plecând cu o nouă parcurgere din următorul nod rămas nevizitat, vom descoperi componenta (4), iar în final (5, 6, 7).

Output final:

4: 0 2 1 3
1: 4
3: 5 6 7

Ultimul pas, după ce am identificat comunităţile existente în cadrul reţelei de socializare, ar fi să putem determina cât de puternică este o astfel de comunitate. Puterea unei comunităţi sau gradul de socializare îl vom determina în funcţie de diametrul comunităţii la care ne referim.

Diametrul unui graf neorientat şi fără costuri pe muchii (în cazul nostru al unei comunităţi) este dat de lungimea celui mai lung drum între oricare două noduri ale sale. Cel mai simplu mod de a calcula diametrul este să efectuăm câte o parcurgere în lăţime din fiecare nod al grafului, reţinând de fiecare dată distanţa celei mai lungi căi descoperite. Cu cât această cale este mai scurtă, cu atât o comunitate este mai unită, deci mai puternică.

Lungimea unei căi de la un nod de start la nodul curent, într-o parcurgere în lăţime, este dată de numărul de noduri intermediare explorate între nodul start şi nodul curent, inclusiv. Pentru a calcula mai uşor distanţa faţă de nodul de start, puteţi să vă folosiţi de relaţia:

                  d(curent) = d(părinte) + 1, curent != start
                  d(curent) = 0,              curent == start

După ce am obţinut diametrul comunităţii vom calcula, pe baza lui, gradul de socializare după cum urmează:

                  g = (N - D) * 100 / (N - 1), N != 1
                  g = 0,                       N == 1
                    N - numărul de utilizatori din comunitate
                    D - diametrul comunităţii

Accesul la această informaţie se va face prin intermediul comenzii PRINT, care va fi apelată cu doi parametri:

• STRENGTH <ID>
  • Comanda va afişa gradul de socializare al comunităţii din care face parte utilizatorul cu id-ul ID. Gradul de socializare se va calcula ca număr întreg, după formula dată.
  • În cazul în care utilizatorul nu există se va afişa textul INEXISTENT.

Pentru simplitate vom folosi acelaşi graf ca în exemplu anterior.

Considerăm ca am primit comanda PRINT STRENGTH 2.

Pasul I

• Izolăm comunitatea din care face parte utilizatorul cu id-ul 2. ⇒ (2, 0, 3, 1), nu neapărat în această ordine
• Stabilim dimensiunea comunităţii. ⇒ N = 4

Pasul II

• Aplicăm BFS din nodul 2. ⇒ D1 = 2, drum maxim (2, 3)
• Aplicăm BFS din nodul 0. ⇒ D2 = 2, drum maxim (0, 1)
• Aplicăm BFS din nodul 3. ⇒ D3 = 3, drum maxim (3, 1)
• Aplicăm BFS din nodul 1. ⇒ D4 = 3, drum maxim (1, 3)

Pasul III

• Alegem D = {max(D_i) | 1 ≤ i ≤ 4}. ⇒ D = 3

Pasul IV

• Calculăm g = (N - D) * 100 / (N - 1). ⇒ g = 33(%)

Output final:

33

Comenzile descrise în secţiunea Cerinţe vor fi citite dintr-un fişier primit ca parametru în terminal. Pentru a putea accesa parametrii cu care a fost lansată în execuţie aplicaţia, Java VM îi pasează metodei public static void main(String[] args), sub forma array-ului args.

Fiecare comandă din fişierul de intrare se va afla pe câte o linie.

Output-ul fiecărei comenzi se va afişa la stdout utilizând metoda System.out.println.

Deoarece Java I/O, în special lucrul cu fişiere, reprezintă un subiect abordat în cea de a doua parte a cursului (Pattern-ul Decorator), vă punem la dispoziţie clasa FileParser care implementează funcţionalităţile de bază pentru citirea din fişiere.

De asemenea, clasa ce va conţine metoda public static void main(String[] args) va trebui să poarte numele Main.

Din punct de vedere logic, reţeaua socială reprezintă o entitate globală, unică. Acest detaliu ne forţează să permitem instanţierea clasei Network o singură dată. Pentru a realiza asta vom folosi pattern-ul Singleton.

Pattern-ul Singleton este un design pattern care restricţionează instanţierea unei clase la un singur obiect. Pattern-ul este folosit adesea în cazuri în care, din punct de vedere logic, design-ul unei aplicaţii nu permite sau nu necesită mai multe instanţe ale unei clase, aşa cum se întâmplă şi în cazul nostru.

Pentru a putea limita instanţierea unei clase la un singur obiect va trebui să marcăm toţi constructorii clasei cu modificatorul de acces private, acest trick impiedicând instaţierea explicită. Atenţie: chiar dacă nu dorim să definim constructor(i) pentru clasa singleton, deoarece constructorul default are modificatorul de acces public, va trebui totuşi să definim un contructor private (cu sau fără parametrii), al cărui corp să nu conţină nici o instrucţiune, pentru a suprascrie constructorul default.

Tot ce ne mai rămâne de făcut este să găsim un mecanism prin care să accesăm, în siguranţă, unica instanţă a clasei singleton. Soluţia este să reţinem această instanţă intern (private), şi să o expunem prin intermediul unei metode publice getInstance(). Cum nu putem apela metoda getInstance() pe un obiect, aceasta va fi precedată de cuvântul-cheie static şi va aparţine clasei. Din considerente de corectitudine, vom utiliza cuvântul-cheie static şi la declararea internă a instanţei.

Singleton.java

public class Singleton {
 
    /* eager instantiation */
    private static final Singleton INSTANCE = new Singleton();
 
    private Singleton() {
        /* initialization code */
    }
 
    /* obtain the one and only instance */
    public static Singleton getInstance() {
        return INSTANCE;
    }
 
}

• 90p trecerea testelor pe Vmchecker
• 10p coding-style, readme, comentarii, organizarea surselor şi a codului, aspect general

Arhiva pe care o veţi urca pe Vmchecker va trebui să conţină în directorul rădăcină:

• directorul cu pachete şi fişiere sursă src, inclusiv
• directorul doc, generat de javadoc
• fişierul README cu descrierea implementării

• Schelet
• Tester
• PDF enunţ temă

• Connected component
• DFS
• BFS
• Singleton pattern
• Javadoc
• Indicații pentru teme
• Coding style