Cuprins
Tema 3: Comoara faraonului
Obiective
- Înţelegerea tehnicilor de programare(Greedy, Programare dinamică, Backtracking)
- Adaptarea acestora la un caz concret
- Alegerea tehnicilor potrivite pentru rezolvare
Informații
- Deadline HARD, 24 mai 2017, ora 23:59 (nu se mai aplica depunctari - acesta este ultimul termen de predare)
- Puteți rezolva tema, dacă doriți, pornind de la scheletul de cod pus la dispoziție aici
- Trimiterea temelor se face pe platforma vmchecker (folosiți credențialele de pe acs.curs.pub.ro).
- Există și un checker local pe care îl puteți descărca de aici
- Pentru întrebări și nelămuriri utilizați forumul asociat temei aici.
Descriere
Un faraon foarte bogat voia să-şi ascundă comorile, aşa că a cerut să i se construiască un seif în forma unei piramide. El a mai cerut ca acesta să aibă o singură intrare (prin vârful piramidei), adică să se poată intra numai urcând pe trepte, şi anumite secvenţe de paşi să blocheze calea de acces (din vârf).
Peste ceva timp, după ce piramida este gata, faraonul vrea să-şi verifice comorile, dar nu-şi mai aminteste pe care trepte trebuie să calce. Faraonul e bătrân şi s-a gândit că va avea problema aceasta, aşa că a cerut următoarele pentru a-i fi mai uşor să găsească drumul:
- să existe cel puţin un drum pe care el poate merge în siguranţă, plecând dintr-un colţ al bazei piramidei
- acest drum să arate la fel, indiferent din ce colţ al bazei pleacă
- să primească o hartă care include un colţ al bazei şi care să-l ajute să găsească drumul
Harta:
- conţine un desen cu o parte din piramidă(atât cât îi trebuie faraonului), pe fiecare treaptă este trecut un număr, iar harta este însoţită de un număr ce va reprezenta o sumă (maximă admisă).
Indicaţii
- desenul de pe hartă poate fi reprezentat folosind o matrice bidimensională pătratică de latură n.
- Pentru fiecare drum, colţul stânga-sus din matrice va fi punctul destinaţie(vârful) şi colţul dreapta-jos din matrice va fi punct de plecare.
- faraonul poate „merge“, în matrice, doar în stânga(câte o coloană) sau în sus(câte o linie) la fiecare pas.
- Excepţie: atunci când, în urma unui pas, ajunge pe o „margine“ din matrice, faraonul poate merge, pentru restul drumului, doar într-un sens: dacă ajunge pe prima linie, mai poate merge doar în stânga(respectiv de pe prima coloană, mai poate merge doar în sus).
- numim drum valid un drum pe care poate „merge“ faraonul (în matrice).
- numim cost al unui drum suma tuturor valorilor din matrice de la poziţiile incluse în acel drum.
- un drum va fi sigur dacă are un cost mai mic decât (sau egal cu) suma maximă admisă.
Cerințe
- Aflaţi costul drumului valid ales după optimul local (la fiecare pas unde are de ales dintre stânga şi sus, alege treapta cu costul mai mic; preferă SUS când costurile sunt egale);
- Aflaţi costul drumului valid ales după optimul global (drumul cu cea mai mică sumă dintre cele posibile);
- Simulaţi un număr de drumuri valide ca încercări pentru a găsi un drum sigur (vă opriţi la primul drum sigur găsit), unde fiecare pas este ales “la întâmplare”(excepţie atunci când există o singură variantă pentru următorul pas - când am ajuns deja pe prima linie sau pe prima coloană)
- (bonus) Aflaţi numărul de drumuri valide sigure.
//cât timp linia (i) != prima linie şi coloana (j) != prima coloană dacă (rand() % 2) Mergi in SUS (linia i-1, coloana j); altfel Mergi in STANGA (linia i, coloana j-1); //pentru restul de paşi (după ce i == prima linie sau j == prima coloană), există un singur sens posibil
- funcţia rand va fi apelată numai în modul descris mai sus şi va fi definită cu următorul cod
//MODULATOR = 2^31 - 1 #define MODULATOR 2147483647 #define MULTIP 1103515245 #define INCREMENT 12345 unsigned int seed = 0; int rand() { seed = (MULTIP * seed + INCREMENT) % MODULATOR; return seed; }
Intrare(Harta):
- C1, C2, C3, C4 = 4 indicatori(vor avea valoarea 1 sau 0 fiecare);
- n = înălţimea piramidei;
- S = suma maximă admisă (pentru ca un drum să fie sigur);
- valorile din matricea(n x n) ce reprezintă piramida;
- nrMaxIncercări = limita pentru a treia cerinţă;
Iesire(fiecare pe un alt rand):
- Dacă (C1 == 1): S1 = suma de la prima cerinţă(drumul obţinut alegând mereu optimul local)
- Dacă (C2 == 1): S2 = suma de la a doua cerinţă(drumul obţinut căutând optimul global)
- Dacă (C3 == 1): nrIncercari sau 0; 0 la ieşire dacă nrIncercari > nrMaxIncercari, nrIncercari la ieşire altfel, unde nrIncercari = numărul de încercări de la a treia cerinţă;
- Dacă (C4 == 1): nrDrumuri = numărul de drumuri valide sigure;
Exemple
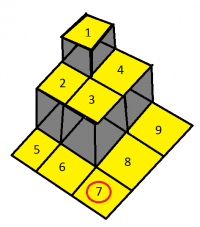
Punctul de plecare: Colţul de la baza piramidei este treapta notată cu 7.
Punctul de sosire: Colţul din vârful piramidei este treapta notată cu 1.
Faraonul ajunge pe o “margine” a hărţii când ajunge pe una din treptele cu valorile 5, 2, 4 sau 9.
matricea asociată acestei hărţi este:
| 1 | 4 | 9 |
| 2 | 3 | 8 |
| 5 | 6 | 7 |
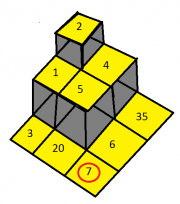
Intrare pentru al doilea desen:
1 1 1 1 3 24 2 4 35 1 5 6 3 20 7 4
- 1 1 1 1 → indicatorii pentru cele 4 cerinţe;
- 3 → n
- 24 → suma maximă admisă;
- 2 4 35 1 5 6 3 20 7 → valorile din matricea (n x n);
- 4 → numărul maxim de încercări pentru cerinţa 3.
Iesire:
21 21 0 2
Explicaţii:
Toate drumurile valide (drumuri pe care poate merge faraonul) sunt:
7->20->3->1->2 Suma = 33 > 24; nesigur 7->20->5->1->2 Suma = 35 > 24; nesigur 7->20->5->4->2 Suma = 38 > 24; nesigur 7->6->5->1->2 Suma = 21 <= 24; sigur 7->6->5->4->2 Suma = 24 <= 24; sigur 7->6->35->4->2 Suma = 54 > 24; nesigur
Dintre cele 6 drumuri, doar 2 sunt sigure (afişat 2 pe ultimul rând la ieşire).
Observam că, pentru acest exemplu, alegerea optimului local duce la acelaşi rezultat cu optimul global (S1 = S2 = 21, afişat pe rândurile 1 şi 2).
Primele 12 valori obţinute la apelul rand() % 2 sunt: 1 1 0 1 0 1 1 1 1 0 0 1. De fapt, veţi ajunge să generaţi numai primele 9 valori (numai de atât aveţi nevoie pentru 4 simulări) pe acest exemplu, după cum urmează:
Prima încercare de drum (primele 2 apeluri rand: 1 1): poziţia = 7, opţiuni = 6 şi 20. SUS -> 6. poziţia = 6, opţiuni = 5 şi 35. SUS -> 35. (Implicit 35->4->2) Soluţia: 7->6->35->4->2 nesigur
A doua încercare de drum (urmatoarele 3 apeluri rand: 0 1 0): poziţia = 7, opţiuni = 6 şi 20. STANGA 20. poziţia = 20, opţiuni = 3 şi 5. SUS 5. poziţia = 5, opţiuni = 1 şi 4. STANGA 1. (Implicit 1->2) Soluţia: 7->20->5->1->2 nesigur
A treia încercare de drum(urmatoarele 2 apeluri rand: 1 1): Aceeaşi situaţie ca la prima incercare Solutia: 7->6->35->4->2 nesigur
A patra încercare de drum(urmatoarele 2 apeluri rand: 1 1): Aceeaşi situaţie ca la prima încercare Solutia: 7->6->35->4->2 nesigur
Deci: nu am găsit niciun drum sigur după nrMaxIncercari = 4 încercări (afişat 0 pe rândul 3).
Variaţii la intrare
21 0
Reguli pentru rulare
- f1 = fişierul cu datele de intrare
- f2 = fişierul de ieşire cu rezultatele cerute
- C1 va fi mereu 1 (prima cerinţă va fi cerută pentru toate cazurile de testare).
- C4 va fi 1 numai pentru testele bonus (30p).
- Pentru 10p, numai C1 va fi 1.
- Pentru alte 20p, numai C1 şi C2 vor fi 1.
- Pentru alte 20p, numai C1 şi C3 vor fi 1.
- Valorile citite de la intrare şi sumele drumurilor vor fi mereu numere naturale din intervalul [0; 1013].
- Pentru 80p, orice drum va avea suma mai mică de 109.
- Pentru toate testele normale, 1 < n < 100 (pentru toate testele bonus, 1 < n < 12).
Reguli pentru trimitere
- Arhiva temei va avea numele GrupaSerie_Nume_Prenume_TemaNr.zip și va fi încărcată pe vmchecker, unde vă puteți loga folosind credențialele de pe acs.curs
- Ea va conține (direct în rădăcină):
- un fişier numit comoara.c sau comoara.cpp
- Makefile-ul (cu regulile make pentru executabilul comoara și clean)
- fișierul README în care va fi descrisă soluția problemei
- Dacă soluția voastră nu compilează, dar ideea este bună și trimiteți o încercare de implementare, puteți primi până la 20p
- Temele care vor fi copiate vor primi 0p