Cuprins
Laborator 02: Algoritmi de sortare 1
1. Obiectivele laboratorului
Propunem studierea următorilor algoritmi de sortare:
- Bubble Sort
- Selection Sort
- Insertion Sort
- Merge Sort
- Quick Sort
2. Introducere
2.1 Calculul complexităţii algoritmilor
Analiza complexității unui algoritm are ca scop estimarea volumului de resurse de calcul necesare pentru execuția algoritmului. Prin resurse se înțelege:
• Spațiul de memorie necesar pentru stocarea datelor pe care le prelucrează algoritmul.
• Timpul necesar pentru execuția tuturor prelucrărilor specificate în algoritm.
Această analiză este utilă pentru a stabili dacă un algoritm utilizează un volum acceptabil de resurse pentru rezolvarea unei probleme. In acest fel timpul de executie va fi exprimat prin numarul de operatii elementare executate. Sunt considerate operatii elementare cele aritmetice (adunare, scadere, ınmulțire, ımpartire), comparatiile si cele logice (negatie, conjuncte și disjunctie).
Este așadar suficient sa se contorizeze doar anumite tipuri de operații elementare, numite operații de bază. Timpul de executie al ıntregului algoritm se obtine ınsumand timpii de executie ai prelucrarilor componente.
Exemplul 1 - Suma a n numere
Consideram problema calculului sumei . Dimensiunea acestei probleme poate fi considerata n. Algoritmul si tabelul cu costurile corespunzatoare prelucrărilor sunt prezentate ın Tabel. Insumand timpii de executie ai prelucrarilor elementare se obtine: T(n)=n(c3 + c4 + c5) + c1 + c2 + c3 deci T(n)=k1n + k2, adica timpul de executie depinde liniar de dimensiunea problemei. Costurile operatiilor elementare influenteaza doar constantele ce intervin ın functia T(n). 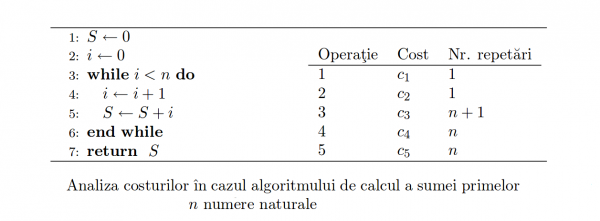
Exemplul 2 - Înmulțirea a 2 matrici
Consideram problema determinarii produsului a doua matrici: A de dimensiune m×n si B de dimensiune n×p. In acest caz dimensiunea problemei este determinata de trei valori: (m, n, p).
In practica nu este necesara o analiza atat de detaliata ci este suficient sa se identifice operatia dominantă si sa se estimeze numarul de repetari ale acesteia. Prin operatie dominanta se ıntelege operatia care contribuie cel mai mult la timpul de executie a algoritmului si de regulă este operatia ce apare ın ciclul cel mai interior. În exemplul ar putea fi considerata ca operatie dominanta, operatia de ınmultire. In acest caz costul executiei algoritmului ar fi T(m, n, p)=mnp
2.2 Caracterizarea unui algoritm
Numim sortare orice aşezare(sau - mai clar - reaşezare) a unor elemente date în aşa fel încât, după aşezare, să existe o ordine completă în funcţie de un atribut(numit cheie) al elementelor.
Pentru a exista o ordine completă, trebuie să alegem o relaţie pe care vrem sa o impunem. Dacă relaţia este valabilă între oricare două elemente pentru care primul element este aşezat la stânga celui de-al doilea, atunci avem o ordine completă.
Exemplu: dacă alegem drept cheie un atribut număr întreg şi relaţia mai mic sau egal(⇐), obţinem ordinea crescătoare.
Vom descrie un algoritm de sortare prin:
- timp mediu - timpul de execuţie la care ne aşteptăm, în medie, pentru sortare
- timp la limită- timpul de execuţie pentru cel mai rău caz posibil
- memorie - memoria maximă de care are nevoie algoritmul pentru sortare(excludem memoria deja alocată înainte de algoritm → vectorul efectiv ce va fi sortat)
- stabilitate - un algoritm stabil păstrează ordinea în care apar două elemente cu aceeaşi cheie(atributul după care sortăm)
Folosim notaţia O(n) pentru a indica:
- un număr de operaţii de ordinul lui n. În acest caz, spunem că avem „complexitate de timp de ordinul lui n“
- o dimensiune de ordinul lui n pentru memoria alocată. În acest caz, spunem că avem „complexitate de spaţiu de ordinul lui n“
2.3 Metodele de sortare folosite
Fiecare algoritm se bazează pe o metodă de sortare:
- Bubble sort - interschimbare
- Selection sort - selecţie
- Insertion sort - inserare
- Merge sort - interclasare
- Quick sort - partiţionare
3. Algoritmii
3.1 Bubble sort
- timp mediu: O(N^2)
- timp la limită: O(N^2)
- memorie: O(1)
- Stabil: DA
Descriere :
Sortarea prin metoda bulelor se consideră drept una din cele mai puţin efective metode de sortare, dar cu un algoritm mai simplu.
- Ideea de bază a sortării prin metoda bulelor este în a parcurge tabloul, de la stânga spre dreapta,
fiind comparate elementele alăturate a[i] si a[i+1]. Dacă vor fi găsite 2 elemente neordonate, valorile lor vor fi interschimbate.
- Parcurgerea tabloului de la stânga spre dreapta se va repeta atât timp cât vor fi întâlnite
elemente neordonate.
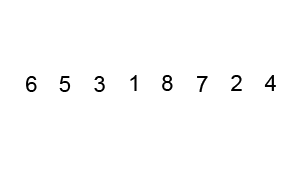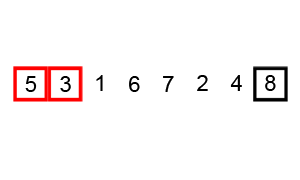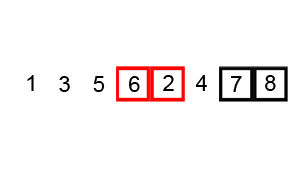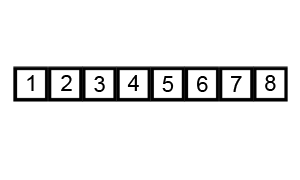
Implementare :
//sortare descrescatoare void bubble(int a[],int n) { int i,schimbat,aux; do { schimbat = 0; // parcurgem vectorul for(i = 0; i < n-1; i++) { // daca valoarea i din vectorul a este mai mica decat cea de pe pozitia i+1 if (a[i] < a[i+1]) { // interschimbare aux = a[i]; a[i] = a[i+1]; a[i+1] = aux; schimbat = 1; } } } while(schimbat); }
3.2 Selection sort
- timp mediu: O(N^2)
- timp la limită: O(N^2)
- memorie: O(1)
- Stabil: DA
Descriere :
Acest algoritm selectează, la fiecare pas i, cel mai mic element din vectorul nesortat(de la poziţia i până la n).Valoarea minimă găsită la pasul i este pusă în vector la poziţia i,facându-se intereschimbarea cu poziţia actuală a minimului.Nu este un algoritm indicat pentru vectorii mari, în majoritatea cazurilor oferind rezultate mai slabe decât insertion sort şi bubble sort. 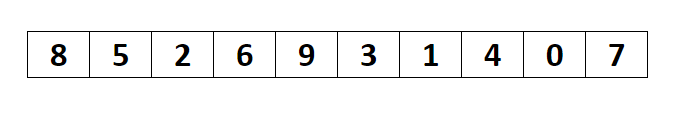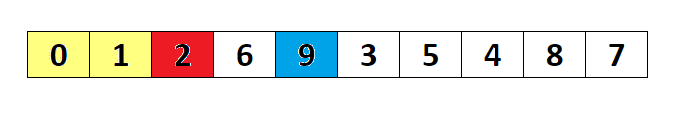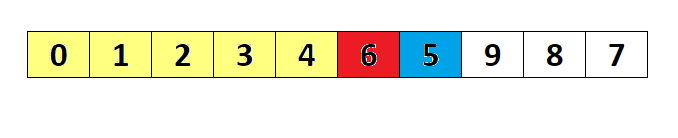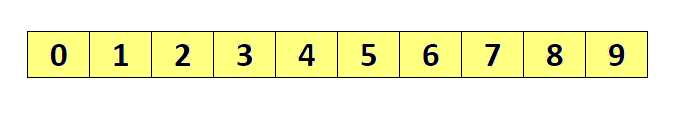
Implementare :
void selectionSort(int a[],int n) { int i,j,aux,min,minPoz; for(i = 0; i < n - 1;i++) { minPoz = i; min = a[i]; for(j = i + 1;j < n;j++) //selectam minimul //din vectorul ramas( de la i+1 la n) { if(min > a[j]) //sortare crescatoare { minPoz = j; //pozitia elementului minim min = a[j]; } } aux = a[i] ; a[i] = a[minPoz]; //interschimbare a[minPoz] = aux; } }
3.3 Insertion sort
- timp mediu: O(N^2)
- timp la limită: O(N^2)
- memorie: O(1)
- Stabil: DA
Descriere :
Spre deosebire de alţi algoritmi de sortare, sortarea prin inserţie este folosită destul de des pentru sortarea tablourilor cu număr mic de elemente. De exemplu, poate fi folosit pentru a îmbunătăţi rutina de sortare rapidă.
- Sortarea prin inserţie seamană oarecum cu sortarea prin selecţie. Tabloul este împărţit
imaginar în două părţi - o parte sortată şi o parte nesortată. La început, partea sortată conţine primul element al tabloului şi partea nesortată conţine restul tabloului.
- La fiecare pas, algoritmul ia primul element din partea nesortată şi il inserează în locul potrivit al părţii sortate.
- Când partea nesortată nu mai are nici un element, algoritmul se opreste.
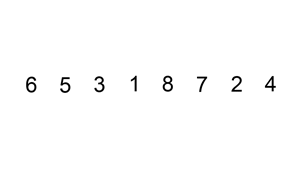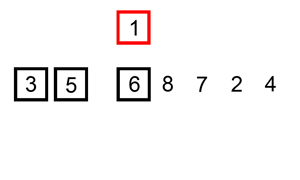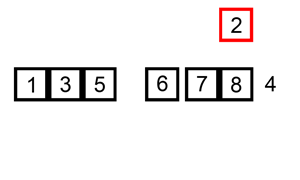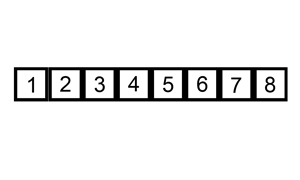
Implementare :
void insertionSort(int a[], int n) { int i, j, aux; for (i = 1; i < n; i++) { j = i; while (j > 0 && a[j - 1] > a[j]) { //cautam pozitia pe care sa mutam a[i] aux = a[j]; //interschimbare a[j] = a[j - 1]; a[--j] = aux; } } }
3.4 Merge sort
- timp mediu: O(N log N)
- timp la limită: O(N log N)
- memorie: O(N)
- Stabil: DA
Descriere :
În cazul sortării prin interclasare, vectorii care se interclasează sunt două secvenţe ordonate din acelaşi vector. Sortarea prin interclasare utilizează metoda Divide et Impera:
- se împarte vectorul în secvenţe din ce în ce mai mici, astfel încât fiecare secvenţă să fie
ordonată la un moment dat şi interclasată cu o altă secvenţă din vector corespunzătoare.
- practic, interclasarea va începe când se ajunge la o secvenţă formată din două elemente. Aceasta, odată ordonată, se va interclasa cu o alta corespunzătoare(cu 2 elemente). Cele două secvenţe vor alcătui un subşir ordonat din vector mai mare(cu 4 elemente) care, la rândul lui, se va interclasa cu un subşir corespunzător(cu 4 elemente) ş.a.m.d.
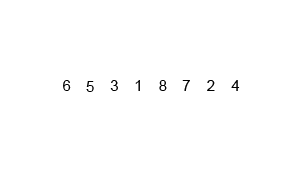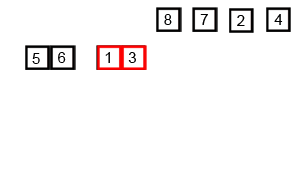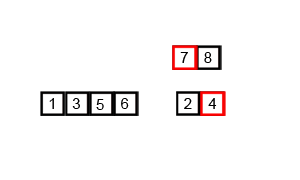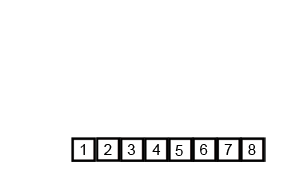
3.5 Quick sort
- timp mediu: O(N log N)
- timp la limită: O(N^2)
- memorie: O(log N)
- Stabil: NU
Descriere :
Quick Sort este unul dintre cei mai rapizi şi mai utilizaţi algoritmi de sortare până în acest moment,bazându-se pe tehnica „Divide et impera“.Deşi cazul cel mai nefavorabil este O(N^2), în practică, QuickSort oferă rezultate mai bune decât restul algoritmilor de sortare din clasa „O(N log N)“.
Algoritmul se bazează pe următorii paşi:
- alegerea unui element pe post de pivot
- parcurgerea vectorului din două părţi(de la stânga la pivot, de la dreapta la pivot, ambele în acelaşi timp)
- interschimbarea elementelor care se află pe „partea greşită“ a pivotului(mutăm la dreapta pivotului elementele mai mari, la stânga pivotului elementel mai mici)
- divizarea algoritmului: după ce mutăm elementele pe „partea corectă“ a pivotului, avem 2 subşiruri de sortat, iar pivotul se află pe poziţia bună.
4. Exerciţii
E0. Alegeţi un algoritm A(dintre Bubble, Insertion şi Selection) şi un algoritm B(dintre Merge şi Quick). Introduceţi nişte variabile globale cu care să contorizaţi numărul de comparaţii pentru algoritmii A şi B. Comparaţi rezultatele pentru un vector de întregi de lungime n = 20.
E1. Implementaţi un algoritm(dintre Bubble, Insertion şi Selection) pentru sortarea unui vector cu n cuvinte de maxim 4 litere fiecare.
E2. Implementaţi un algoritm(dintre Merge şi Quick) pentru sortarea unui vector de structuri, unde fiecare structură reprezintă un moment de timp(int ora,min,sec).
E3. Se dă un vector de n întregi, iar toate valorile din vector sunt între 0 şi 1000. Sortaţi vectorul în timp O(n).
Puteţi utiliza următorul model pentru exerciţiile propuse: scheletsortare.zip
5. Exerciţii de laborator (Linux)
Pentru acest laborator puteți descărca scheletul de cod de aici. Descărcați arhiva și dezarhivați-o.
Linux
Puteti folosi utilitarul wget pentru descarcare si utilitarul unzip pentru dezarhivare.
wget http://elf.cs.pub.ro/sda-ab/wiki/_media/laboratoare/lab8_sortari-skel.zipunzip lab8_sortari-skel.zip
Pentru compilare folositi comanda make. Pentru rulare puteti folosi comanda make run sau ./sort.
