Cuprins
Laborator 06: Introducere în teoria grafurilor
1 Obiectivele laboratorului
- Definirea structurii și elementelor unui graf neorientat
- Definirea structurii și elementelor unui graf orientat
2 Grafuri neorientate
2.1 Definiție
Un graf neorientat este o pereche ordonată de multimi(X,U),unde:
- X este o mulțime finită și nevidă de elemente numite noduri sau vârfuri
- U este o mulțime de perechi neordonate din X,numite muchii
2.2 Structură
Un graf are următoarele elemente:
- Mulțimea nodurilor X - Mulțimea tuturor nodurilor grafului
- Multimea muchiilor U - Mulțimea tuturor muchiilor grafului
- Gradul nodului - numărul de muchii formate cu ajutorul nodului respectiv
- Nod izolat - Un nod ce nu formează nici-o muchie
- Noduri terminale - Un nod ce formează o singură muchie
- Noduri adiacente - Noduri intre care există o muchie
- Nod si muchie incidente - Nodul face parte dintr-o muchie
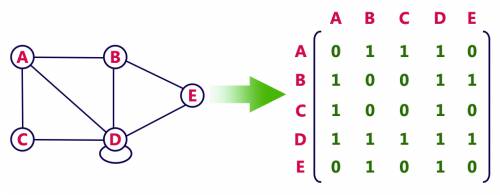
2.3 Reprezentare
- Matricea de adiacență - este o matrice a cu n linii și n coloane,în care elementele a[i,j] se definesc astfel:
- a[i,j] = 1 ,dacă ∃ muchia [i,j] cu i≠j
- a[i,j] = 0 ,în caz contrar
- Lista de adiacență - este un tablou de liste egal cu numarul de varfuri;dacă există o muchie intre nodul curent si un alt nod,atunci acesta se trece în listă
- Vectorul de muchii - mulțime ce conține toate muchiile grafului
Având lista de adiacentă:
- A:B→C→D
- B:A→D→E
- C:A→D
- D:A→B→C→D→E
- E:B→D
Se numeşte lanţ elementar un lanţ în care nu se repetă vârfuri.
Se numeşte lanţ simplu un lanţ în care nu se repetă muchii.
Se numeşte ciclu un lanţ simplu pentru care primul şi ultimul vârf coincid.
Se numeşte ciclu elementar un ciclu în care nu se repetă vârfuri(excepţie primul şi ultimul).
3 Grafuri orientate
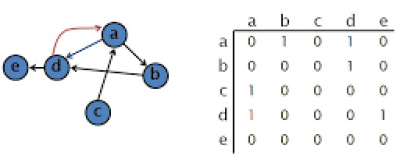
3.1 Definiție
Un graf orientat este o pereche ordonată de mulțimi G={X,U},unde:
- X este o mulțime finită și nevidă numită mulțimea nodurilor(vârfurilor)
- U este o mulțime formată din perechi ordonate de elemente ale lui X,numită mulțimea arcelor
3.2 Structură
Într-un graf orientat, distingem:
- gradul interior/intern al unui nod: numărul de arce care intră în nod
- gradul exterior/extern al unui nod: numărul de arce care ies din nod
3.3 Reprezentare
Matricea de adiacență - este o matrice a cu n linii și n coloane,în care elementele a[i,j] se definesc astfel:
- a[i,j] = 1 ,dacă ∃ arcul (i,j) în mulțimea U
- a[i,j] = 0 ,în caz contrar
Matricea vârfuri-arce este o matrice B cu n = |X| linii și m = |U| coloane,în care fiecare element b[i,j] este:
- 1 ,dacă nodul i este o extremitate inițială a arcului
- -1 ,dacă nodul i este o extremitate finală a arcului
- 0 ,dacă nodul i nu este o extremitate a arcului
4 Parcurgerea grafurilor
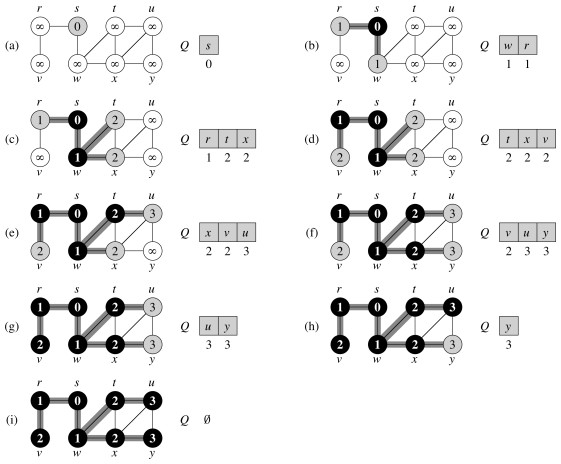
4.1 Parcurgerea în lățime
Parcurgerea în lățime (Breadth-First-Search -BFS) este o metodă ce presupune vizitarea nodurilor în următoarea ordine:
- nodul sursă (considerat a fi pe nivelul 0)
- vecinii nodului sursă (reprezentând nivelul 1)
- vecinii încă nevizitați ai nodurilor de pe nivelul 1 (reprezentând nivelul 2)
- ș.a.m.d
4.1.1 Implementare
Pe masură ce algoritmul avansează,se colorează nodurile în felul următor:
- alb - nodul este nedescoperit încă
- gri - nodul a fost descoperit și este în curs de procesare
- negru - procesarea nodului s-a încheiat
Se păstrează informațiile despre distanța până la nodul sursă. Se obține arborele BFS
Pentru implementarea BFS se utilizează o coadă (Q) în care inițial se află doar nodul sursă.Se vizitează pe rând vecinii acestui nod și se pun și ei în coadă.În momentul în care nu mai există vecini nevizitați,nodul sursă este scos din coadă.
Pentru fiecare nod u din graf { culoare[u]=alb d[u] = infinit //in d se retine distanta pana la nodul sursa p[u] = null // } culoare[sursă]=gri d[sursă]=0 enqueue(Q,sursă) //punem nodul sursă în coada Q Cât timp coada Q nu este vidă { v=dequeue(Q) //extragem nodul v din coadă pentru fiecare u dintre vecinii lui v dacă culoare[u] == alb { culoare[u] = gri p[u] = v d[u] = d[v] + 1 enqueue(Q,u) //adăugăm nodul u în coadă } culoare[v] = negru //am terminat explorarea vecinilor lui v }
4.2 Parcurgerea în adâncime
Parcurgea în adâncime (Depth-First-Search -DFS) presupune explorarea nodurilor în următoarea ordine:
- Nodul sursă
- Primul vecin nevizitat al nodului sursă (îl numim V1)
- Primul vecin nevizitat al lui V1 (îl numim V2)
- ș.a.m.d
- În momentul în care am epuizat vecinii unui nod Vn, continuăm cu următorul vecin nevizitat al nodului anterior,Vn-1
Această metoda de parcurgere pune prioritate pe explorarea în adâncime (pe distanțe tot mai mari față de nodul sursă).
4.2.1 Implementare
Spre deosebire de BFS, DFS utilizează o stivă în loc de o coadă. Putem defini o stivă sau ne putem folosi de stiva compilatorului, prin apeluri recursive.
funcţie pasDFS(curent) { pentru fiecare u dintre vecinii nodului curent dacă culoare[u] == alb { culoare[u] = gri p[u] = curent d[u] = d[curent] + 1 pasDFS(u); //adăugăm nodul u în "stivă" şi începem explorarea } culoare[curent] = negru //am terminat explorarea vecinilor nodului curent //ieşirea din funcţie este echivalentă cu eliminarea unui element din stivă } Pentru fiecare nod u din graf { culoare[u]=alb d[u] = infinit //in d se retine distanta pana la nodul sursa p[u] = null } culoare[sursă] = gri; d[sursă] = 0; //se apelează iniţial pasDFS(sursă)
5. Exerciţii
Implementaţi, pentru fiecare cerinţă, câte o funcţie care:
- creează matricea de adiacenţă pentru un graf neorientat cu N noduri, folosindu-se de o listă(sau o matrice cu 2 coloane) de muchii(la alegere - muchiile citite în funcţie sau primite printr-un parametru).
- calculează gradul fiecărui nod. Afişaţi numărul de noduri izolate şi numărul de noduri terminale.
- primeşte un şir de noduri şi verifică dacă acesta poate reprezenta un lanţ.
- primeşte un şir de noduri şi afişează matricea de adiacenţă a subgrafului format cu nodurile respective
- afişează matricea de adiacenţă a unui graf orientat construit astfel:
- graful orientat are atâtea arce câte muchii are graful neorientat
- există arc în graful orientat între două noduri daca şi numai dacă există muchie între aceleaşi noduri în graful neorientat.
- Extra - câte astfel de grafuri orientate pot fi formate?
Cerinţele 2, 3, 4 şi 5 se vor folosi de matricea de adiacenţă a grafului de la cerinţa 1.
5.1. Exerciții - schelet de laborator
Pentru acest laborator puteți descărca scheletul de cod de aici. Descărcați arhiva și dezarhivați-o.
Linux
Puteti folosi utilitarul wget pentru descarcare si utilitarul unzip pentru dezarhivare.
wget http://elf.cs.pub.ro/sda-ab/wiki/_media/laboratoare/lab5_grafuri-skel.zipunzip lab5_grafuri-skel.zip
Pentru compilare folositi comanda make. Pentru rulare puteti folosi comanda make run sau ./graph.
De interviu
- Plecând dintr-un nod K, verificaţi dacă puteţi găsi un ciclu în graf.
- Verificaţi dacă există un lanţ care uneşte nodurile sursă(S) şi destinaţie(D). Dacă există, cum puteţi găsi lanţul cu număr minim de muchii?
- Verificaţi dacă există un lanţ hamiltonian în graf.
- Verificaţi dacă există un lanţ eulerian în graf.
- Verificaţi dacă o muchie dată (A, B) este un pod pentru drumul de la S la D.
Un lanţ hamiltonian este un lanţ elementar(nu se repetă nodurile) care trece prin fiecare nod.
Un lanţ eulerian este un lanţ simplu(nu se repetă muchiile) care trece prin fiecare muchie.
Spunem că muchia (A, B) este pod pentru drumul de la S la D dacă orice lanţ care duce de la S la D trece prin muchia (A, B).